Algorithmica HPC研读记录（1-3章）

一、复杂性模型

概述

传统复杂性理论

To estimate the real running time of a program, you need to sum all latencies for its executed instructions and divide it by the clock frequency, that is, the number of cycles a particular CPU does per second.

为了计算实际的程序运行时间，需要把所有指令的延迟都累加起来。“以时钟频率划分”指的是通过将程序执行过程中所有指令的延迟时间（latencies）除以CPU的时钟频率，来估算程序的实际运行时间。

时钟频率（Clock Frequency）：时钟频率是指CPU每秒钟能够执行多少个时钟周期，单位通常是赫兹（Hz）。例如，如果一个CPU的时钟频率是 3 GHz，那就意味着它每秒钟可以执行 30 亿个时钟周期。
延迟（Latency）：每条指令在执行时都有一个延迟，表示从开始执行到完成所需的时间。这个延迟通常是以时钟周期为单位的。例如，如果某条指令需要 5 个时钟周期来执行，那么它的延迟就是 5 个周期。
以时钟频率划分的意思：当你想要计算程序的总运行时间时，你需要将所有指令的延迟加起来，得到总的延迟周期数。然后，为了将这个延迟周期转换为时间，你就需要将总的延迟周期数除以时钟频率。这是因为时钟频率告诉你 CPU 每秒钟执行多少个时钟周期，从而你可以通过除法将延迟周期转换为实际的时间（单位为秒）。

假设某程序的指令总延迟为 100,000 个时钟周期，而 CPU 的时钟频率是 2 GHz（即每秒 20 亿个周期），那么程序的实际运行时间可以通过以下公式计算：

$运行时间延迟周期数时钟频率秒秒$

通过这种方式，可以估算程序的实际运行时间，考虑到不同指令的执行延迟和CPU的时钟频率。

渐进分析理论

在计算机发展的初期，计算机科学家需要密切关注程序的执行时间、所用的处理周期（即基本的计算单元）以及涉及的操作次数。这些详细的度量在当时非常重要，因为计算资源有限，性能优化对程序的运行有显著的影响。

随着计算机性能的提升，系统变得更强大，详细的执行时间、周期和操作数的度量变得不那么关键。计算机科学家转而更加关注渐近分析（Asymptotic Analysis），这种分析方法提供了一个抽象的视角，用来描述算法在输入规模增大时的性能变化。

例如，计算机科学家不再一一跟踪每一个操作和周期，而是使用“大 O”符号来描述一个算法随着输入规模增长的运行时间表现。这种方法让你可以忽略常数因素和较低阶的项，专注于算法如何随着输入的增大而扩展。

使用渐近复杂度（例如 Big O、Big Theta 和 Big Omega）使得研究人员和工程师可以专注于算法效率的“整体情况”。这种方法抹去了硬件性能和初始操作成本的细节，让人们能够更加容易地比较不同算法，而不需要考虑具体实现或硬件差异的影响。

Big O、Big Theta 和 Big Omega 是用于描述算法时间复杂度的渐近符号，它们分别表示不同方面的性能分析。它们的主要区别在于描述算法的上界、下界和精确度。以下是对这三者的详细解释：

Big O (大 O)

定义：Big O 符号用于表示算法的上界，即算法的 最坏情况 时间复杂度。
含义：Big O 描述的是随着输入规模增大，算法的运行时间增长的速度。它给出了一个上限，说明在最坏情况下，算法的执行时间不会超过某个特定的增长速率。
表示法：如果某个算法的时间复杂度是 O(f(n))，意味着对于足够大的输入 n，算法的时间复杂度最多是 f(n) 的一个常数倍，忽略常数因素。
例子：假设算法的时间复杂度为 O(n^2)，这意味着随着输入规模 n 增加，算法的运行时间最多增长到与 n^2 成正比。

$对于足够大的$

其中，C 是常数，n 是输入规模。

Big Theta (大 Θ)

定义：Big Theta 符号用于表示算法的精确时间复杂度，或者说它给出了一个算法时间复杂度的 上下界。
含义：Big Theta 描述的是算法的时间复杂度的 渐近精确界限，即算法的执行时间随着输入规模增大时，会以 f(n) 作为界限的上下界增长。
表示法：如果某个算法的时间复杂度是 Θ(f(n))，意味着该算法在最坏和最好情况下的时间复杂度都与 f(n) 成正比，并且在足够大的输入规模下，算法的时间复杂度将在 f(n) 的一个常数范围内波动。
例子：如果某个算法的时间复杂度是 Θ(n log n)，这意味着无论最坏情况还是最好情况，它的时间复杂度都是与 n log n 成正比的。

$对于足够大的$

其中，C₁ 和 C₂ 是常数，n 是输入规模。

Big Omega (大 Ω)

定义：Big Omega 符号用于表示算法的下界，即算法的 最好情况 时间复杂度。
含义：Big Omega 描述的是在最好的情况下，算法的时间复杂度的最小增长速率。它给出了一个算法执行所需时间的下限，表示即使在最理想的情况下，算法的执行时间也不会低于某个特定的增长速率。
表示法：如果某个算法的时间复杂度是 Ω(f(n))，意味着对于足够大的输入规模 n，算法的时间复杂度至少会增长到与 f(n) 成正比的某个常数倍。
例子：如果某个算法的时间复杂度是 Ω(n)，这意味着在最佳情况下，算法的运行时间至少与 n 成正比。

$对于足够大的$

其中，C 是常数，n 是输入规模。

总结来说，从精确计算操作数到使用渐近复杂度分析的转变，是计算机硬件性能提高的结果，表明对于大规模输入来说，算法的扩展行为比具体的时间或操作数更为重要。

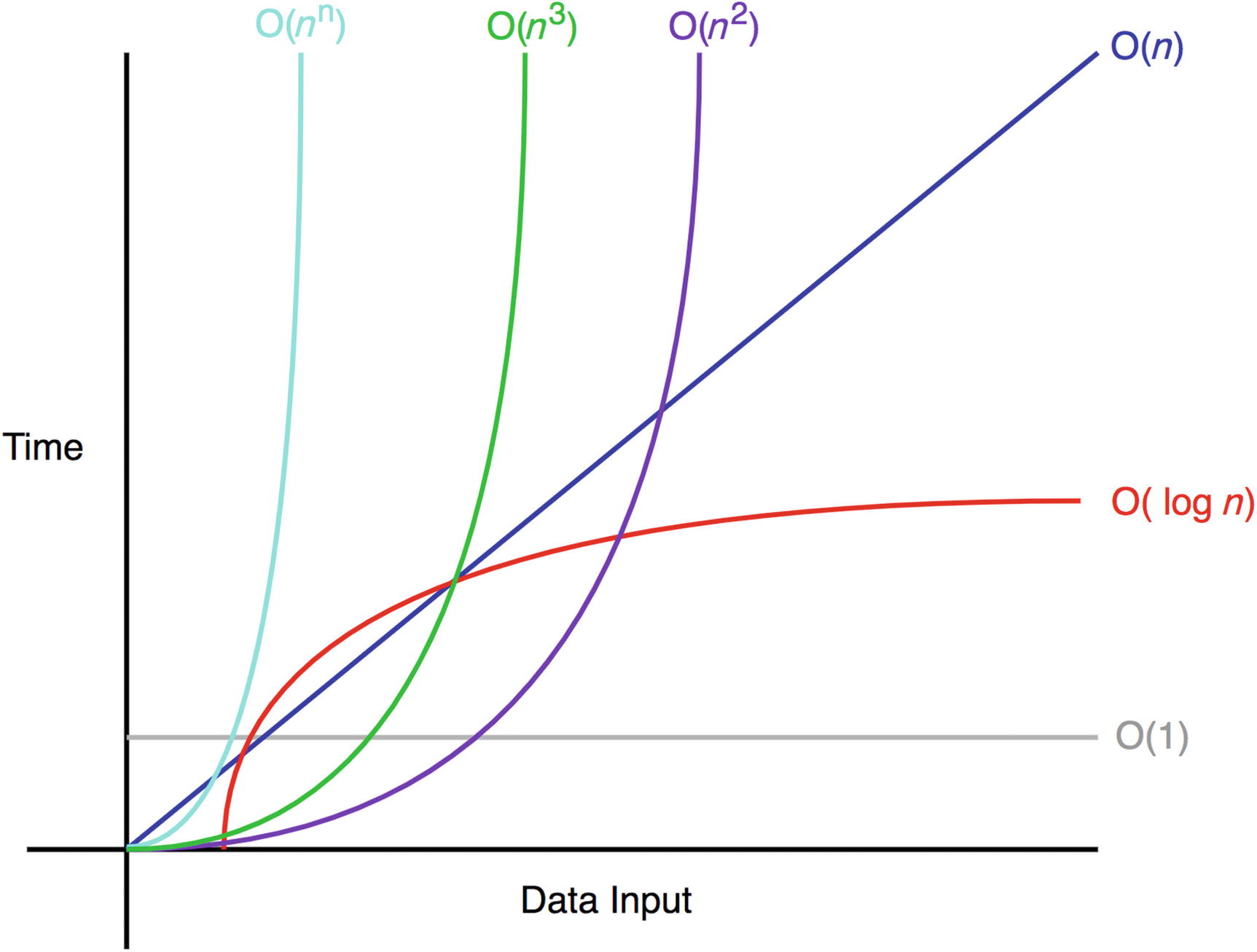
Under the promise that computers will eventually become fast enough to handle any sufficiently large input in a reasonable amount of time, asymptotically faster algorithms will always be faster in real-time too, regardless of the hidden constant.

But this promise turned out to be not true — at least not in terms of clock speeds and instruction latencies — and in this chapter, we will try to explain why and how to deal with it.

这里存在一个假设，就是在渐进分析上更快的算法会在实际运行时间上也会更快。但这个假设实际上是错误的，之后具体的篇章讲述了详细的原因以及处理方式。

现代硬件

芯片的出现极大降低了电脑的成本，是一个革命性的发明。微芯片的制造过程，主要是通过光刻（photolithography）技术在晶体硅片上“打印”电路。

根据Dennard Scaling理论，当晶体管尺寸缩小约30%时，会发生以下变化：

晶体管密度翻倍：晶体管数量增加，能在相同面积内放置更多的晶体管。因为
时钟速度增加40%：由于晶体管变小，其开关速度加快，时钟频率能够提高。因为
功率密度保持不变：虽然晶体管数量增加，但由于每个晶体管功耗减少，总体功耗密度（单位面积的功耗）保持相对不变。

Gordon Moore在1975年就做出了预测，晶体管上微处理器的数量每两年就会翻一番。这就是我们熟知的摩尔定律。

上述两个理论都不是物理定律，它们都是专家的观测结果，在某种程度上一定会受到基础物理的制约。

Thermodynamically, a computer is just a very efficient device for converting electrical power into heat. This heat eventually needs to be removed, and there are physical limits to how much power you can dissipate from a millimeter-scale crystal. Computer engineers, aiming to maximize performance, essentially just choose the maximum possible clock rate so that the overall power consumption stays the same. If transistors become smaller, they have less capacitance, meaning less required voltage to flip them, which in turn allows increasing the clock rate.

计算机的热力学本质：

从热力学的角度来看，计算机实际上就是一种非常高效的设备，将电能转化为热能。
计算机在运行过程中会消耗电能并生成热量，随着功耗的增加，热量也会增加。因此，必须通过适当的散热机制将热量排除，否则过多的热量会影响计算机的稳定性和性能。

功耗与散热的物理限制：

物理限制：计算机的功耗有一定的物理限制，特别是在微米尺度的晶体管上。随着晶体管的尺寸变小，每个晶体管产生的热量会增加，而散热能力是有限的。因此，需要有效的散热设计来避免温度过高，导致计算机性能下降或硬件损坏。

计算机工程师的设计目标：

在设计中，工程师们通常会选择最大可能的时钟频率，以保证在给定的功耗限制内，计算机能够提供尽可能高的性能。时钟频率越高，芯片每秒钟能够执行的操作就越多，从而提高计算能力。

晶体管尺寸对性能的影响：

当晶体管变得更小时，电容变小，这意味着晶体管的开关所需的电压变低。因此，电压要求降低，进而可以提高时钟频率。更高的时钟频率意味着芯片能够在单位时间内处理更多的任务，从而提升计算性能。

但2005年到2007年间，随着晶体管尺寸进一步缩小，漏电效应（leakage effects）导致了微芯片设计面临的一个新的问题，使得之前依赖于缩小晶体管来提升性能的策略不再有效。

漏电效应（Leakage Effects）：

晶体管尺寸过小：随着微芯片中的晶体管变得越来越小，电路的特征尺寸接近于纳米级别。这使得晶体管和周围电路之间的相互作用变得复杂，导致出现了漏电效应。
磁场干扰：当晶体管的尺寸足够小，晶体管产生的电磁场开始影响到相邻电路中的电子运动。电场和磁场的干扰可能会导致电子朝着不该去的方向运动，进而引发不必要的加热和比特翻转（bit flipping）。

不必要的加热：

晶体管本应按照设计工作，但由于电流的误导，电子可能在错误的路径上流动，造成额外的热量产生。这不仅增加了能量消耗，还使得芯片的散热负担增加，进而影响芯片的稳定性。

比特翻转（Bit Flipping）：

由于电流干扰和漏电效应，某些电子可能会被错误地推动到其他状态，这会导致比特翻转。比特翻转指的是存储的数据位发生错误，从而可能导致计算错误或系统故障。

一种应对漏电效应的有效方法是增加电压，但是增加电压会导致功耗增加以及时钟频率降低。这样一来微型化的优势就开始减弱了。

Here are some core approaches making use of more available transistors that are driving recent computer designs:

Overlapping the execution of instructions so that different parts of the CPU are kept busy (pipelining);

Executing operations without necessarily waiting for the previous ones to complete (speculative and out-of-order execution);

Adding multiple execution units to process independent operations simultaneously (superscalar processors);

Increasing the machine word size, to the point of adding instructions capable of executing the same operation on a block of 128, 256, or 512 bits of data split into groups (SIMD);

Adding layers of cache on the chip to speed up RAM and external memory access time (memory doesn’t quite follow the laws of silicon scaling);

Adding multiple identical cores on a chip (parallel computing, GPUs);

Using multiple chips in a motherboard and multiple cheaper computers in a data center (distributed computing);

Using custom hardware to solve a specific problem with better chip utilization (ASICs, FPGAs).

以上列出了几种核心的计算机设计方法，利用更多可用的晶体管来推动近期计算机设计的进展。

流水线技术（Pipelining）

原理：流水线技术将指令的执行分为多个阶段，使得每个阶段可以同时处理不同的指令。这样可以减少等待时间并提高执行效率。
优势：通过重叠执行不同指令的不同部分，CPU的各个部分保持工作状态，提升了指令执行的并行度。

猜测执行和乱序执行（Speculative and Out-of-Order Execution）

原理：在某些指令尚未完成时，处理器会提前执行一些推测的操作，或者不必等待前一条指令完成后才执行下一条指令。
优势：提高了执行效率，减少了等待时间，尤其是在指令之间没有强依赖关系时。

超标量处理器（Superscalar Processors）

原理：通过在处理器中添加多个执行单元，允许同时处理多个独立的操作。
优势：可以在每个时钟周期内并行执行多个指令，提升了计算能力。

SIMD（Single Instruction, Multiple Data）

原理：增加机器字长，使得处理器能够对128位、256位或512位的数据块进行操作，并对这些数据分组处理。
优势：在进行数据处理时，同一指令可以同时操作多个数据，极大提高了处理能力，特别是在大规模数据并行处理（如图像和视频处理）时非常有效。

多级缓存（Multiple Layers of Cache）

原理：在芯片上添加多个层级的缓存，以加速RAM和外部内存的访问速度。
优势：由于内存访问速度相对较慢，通过高速缓存可以显著减少CPU与内存之间的访问延迟，提升整体性能。

多核处理（Parallel Computing, GPUs）

原理：在芯片上添加多个相同的核心，允许同时处理多个任务或线程，适用于并行计算任务。
优势：可以显著提升多任务处理能力，尤其适用于GPU计算（如图形渲染、深度学习等并行任务）。

分布式计算（Distributed Computing）

原理：使用多个芯片在主板上，或者在数据中心中使用多个便宜的计算机进行分布式计算。
优势：通过将任务分配到多个计算节点，可以有效扩展计算能力，尤其适用于大规模数据处理和高性能计算。

定制硬件（ASICs, FPGAs）

原理：使用定制的硬件（如ASIC和FPGA）来解决特定问题，以便在特定任务中获得更好的芯片利用率和性能。
优势：通过硬件的专门设计，可以为特定应用提供更高的性能和更低的功耗，广泛应用于加速特定计算任务，如加密算法、图像处理等。

对于现代计算机来说，传统的“计算所有操作”来预测算法性能的方法不仅仅是有一点偏差，而是误差可能达到几个数量级。这表明我们需要采用新的计算模型和其他方式来评估算法的性能。

编程语言

The real answer, of course, is much more complicated and highly dependent on what kind of “operation” you have in mind. It can be as low as 10^7 for things like pointer chasing and as high as 10^11 for SIMD-accelerated linear algebra.

这个对比旨在强调，在不同的硬件和操作类型下，算法的表现可能会有巨大的差异，单纯计算操作次数并不足以准确预测实际性能。在这里，更多的操作次数（10^11） 并不一定意味着更花时间，反而通过现代的硬件加速技术（如 SIMD），高效的并行计算能在短时间内处理更多操作。

so one of the first things people did after creating computers was create programming languages, which abstract away some details of how computers operate to simplify the process of programming.

人们在创造了计算机后第一件事就是创建编程语言，因为这能隐藏执行细节并简化编程过程。而编程语言具有不同的类型。

从程序员的角度来看：

编译型语言（Compiled Languages）：这类语言在执行之前会经过一个预处理阶段（编译），即把源代码转换为机器代码，然后直接执行。比如 C、Go、Rust 等语言。编译型语言通常执行效率较高，因为它们的代码已经完全被转换成了 CPU 可以直接理解的机器代码。
解释型语言（Interpreted Languages）：解释型语言的执行是在运行时进行的，程序并不会提前转换为机器代码，而是通过一个叫做解释器的程序逐行执行源代码。典型的解释型语言有 Python、JavaScript 和 Ruby。这类语言的优点是方便调试和动态执行，但通常速度较慢，因为每一行代码都需要实时解释执行。

从计算机的角度来看：

原生语言（Native Languages）：原生语言直接生成机器代码，能够直接在 CPU 上执行，运行时不依赖其他中间层。像 C、Go 和 Rust 这样的编译型语言就属于原生语言，因为它们直接生成可以被操作系统和 CPU 执行的机器码。
托管语言（Managed Languages）：托管语言依赖某种运行时（runtime）来进行执行。运行时负责管理内存、执行代码等操作。Java、C# 和 Erlang 就是典型的托管语言，它们在执行之前会被编译成一种中间代码，然后由虚拟机（VM）来执行。比如 Java 代码会先被编译为字节码（bytecode），然后由 JVM 运行。

根据上述的分类方式，编程语言可以分为三大类：

解释型语言（Interpreted Languages）：比如 Python、JavaScript、Ruby 等。直接在运行时由解释器执行代码。
带有运行时的编译语言（Compiled Languages with a Runtime）：如 Java、C#、Erlang 等。源代码首先被编译为中间代码（比如字节码），然后由虚拟机或运行时执行。
编译后的原生语言（Compiled Native Languages）：如 C、Go、Rust 等。直接编译成机器代码，可以直接在 CPU 上运行。

为了直观感受这三类语言效率上的差距，我们可以以1024*1024规模的矩阵相乘来测试一下执行效率：

解释型语言（以python为例）

import time
import random

n = 1024

a = [[random.random()
      for row in range(n)]
      for col in range(n)]

b = [[random.random()
      for row in range(n)]
      for col in range(n)]

c = [[0
      for row in range(n)]
      for col in range(n)]

start = time.time()

for i in range(n):
    for j in range(n):
        for k in range(n):
            c[i][j] += a[i][k] * b[k][j]

duration = time.time() - start
print(duration)

我自己跑出来的结果大约是181秒左右。然后我们仔细看看发生了什么。

首先解释器开始解析c[i][j] += a[i][k] * b[k][j] 这一个语句，然后去找a，b，c是什么类型。
找到a是一个列表，然后提取出[]的操作符，解析出a[i]，这仍然是一个列表，于是继续解析a[i][k]，这是一个float类型的数
之后取出并执行*操作
对b和c进行同样的解析，最终把结果存在c[i][j]

然后我们来看看托管语言（Managed Languages），以java为例

// Matmul.java
import java.util.Random;

public class Matmul {
    static int n = 1024;
    static double[][] a = new double[n][n];
    static double[][] b = new double[n][n];
    static double[][] c = new double[n][n];

    public static void main(String[] args) {
        Random rand = new Random();

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                a[i][j] = rand.nextDouble();
                b[i][j] = rand.nextDouble();
                c[i][j] = 0;
            }
        }

        long start = System.nanoTime();

        for (int i = 0; i < n; i++)
            for (int j = 0; j < n; j++)
                for (int k = 0; k < n; k++)
                    c[i][j] += a[i][k] * b[k][j];
                
        double diff = (System.nanoTime() - start) * 1e-9;
        System.out.println(diff);
    }
}

javac Matmul.java
java Matmul

这仅仅用了2.4秒就完成了。

java 程序首先会被编译成 字节码，即 .class 文件。这些字节码不是针对某一特定硬件架构的机器码，而是跨平台的。字节码可以在任何支持 JVM 的平台上运行。字节码在 JVM（Java Virtual Machine）中解释执行。JVM 是一个运行 Java 程序的虚拟机，它将字节码转换为适合当前硬件的机器指令。由于字节码不是直接的机器码，所以 JVM 执行过程会有一定的性能开销。

python也有类似于JVM的技术，称为PyPy。

然后最后我们看看编译型语言，如C。

#include <stdlib.h>
#include <stdio.h>
#include <time.h>

#define n 1024
double a[n][n], b[n][n], c[n][n];

int main() {
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            a[i][j] = (double) rand() / RAND_MAX;
            b[i][j] = (double) rand() / RAND_MAX;
        }
    }

    clock_t start = clock();

    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            for (int k = 0; k < n; k++)
                c[i][j] += a[i][k] * b[k][j];

    float seconds = (float) (clock() - start) / CLOCKS_PER_SEC;
    printf("%.4f\n", seconds);
    
    return 0;
}

gcc -O3 -g test.c -o test	#我们开O3优化进行编译
./poc

只用了1.3秒就得到了结果。如果我们换为gcc -O3 -march=native -ffast-math -g poc.c -o poc，甚至可以在0.15秒左右的时间内得到结果。

-march=native 标志告诉编译器将代码优化为运行在当前编译机器的CPU架构上。这意味着编译器会针对当前处理器的指令集和特定功能进行优化，利用特定的硬件指令来提升性能。

例如，现代CPU支持高级向量化指令（如 AVX、SSE），可以一次性处理多个数据元素，从而加速计算。使用 -march=native 标志后，编译器会利用这些指令，从而大幅提升性能。

-ffast-math 标志允许编译器进行激进的浮点优化，例如放宽浮点数的舍入和精度要求。虽然这可能会引入一些不精确的计算，但也可以显著加速数学运算，使得编译器能够使用更快的（但精度较低的）浮点计算。

编译器还可以重新安排浮点操作，以避免一些昂贵的操作，或者利用硬件特定指令，例如用于并行操作的向量化指令。

我们现在回到python，但是使用 OpenBLAS来进行计算：

import time
import numpy as np

n = 1024

a = np.random.rand(n, n)
b = np.random.rand(n, n)

start = time.time()

c = np.dot(a, b)

duration = time.time() - start
print(duration)

所用时间来到了惊人的0.02秒。OpenBLAS 是一个广泛使用的高效线性代数库，通常用于实现像矩阵乘法这样的操作。为了实现优化，OpenBLAS中关于稠密矩阵乘法的实现通常涉及大量手写的汇编代码，每种架构的代码都需要根据其硬件特性单独定制。这些实现可能有多达 5000行汇编代码，针对不同的硬件架构进行了深度优化，以充分利用其特性（如SIMD指令集、缓存优化等）。后续的内容将逐步解释如何利用一些优化技术来提升矩阵乘法的性能。最终的目标是开发出一种简化的矩阵乘法实现，仅需 不到40行C代码，并能够在性能上接近OpenBLAS的实现。

二、计算机架构

指令集架构（ISA）

Hardware engineers love abstractions too. An abstraction of a CPU is called an instruction set architecture (ISA), and it defines how a computer should work from a programmer’s perspective. Similar to software interfaces, it gives computer engineers the ability to improve on existing CPU designs while also giving its users — us, programmers — the confidence that things that worked before won’t break on newer chips.

指令集架构（ISA）就像软件中的接口一样，规定了硬件需要支持的指令和功能。硬件工程师根据这个架构设计和实现具体的CPU，确保每个指令能够正确执行，而程序员则通过这些指令集来编写代码，而不需要关心底层硬件的具体实现细节。假设我们使用的是基于 x86 架构的 CPU。这个架构定义了一些基本的指令，如 MOV（移动数据）、ADD（加法）、JMP（跳转）等。无论你用什么样的 x86 处理器，这些指令的语义和功能始终保持一致。

指令集不同于字符编码集或即时通讯协议一样，能够低成本地在一台机器上完整的分别支持每一个不同的集合。一般机器会支持arm(RISC)或者x86(CISC)架构其中之一。

ARM架构被广泛应用于几乎所有的移动设备，如智能手机、平板电脑等。此外，还应用于一些智能设备和计算设备，包括电视、智能冰箱、微波炉、汽车自动驾驶系统等。因为ARM架构的处理器通常采用低功耗设计，适合移动设备和嵌入式设备使用。

x86架构几乎被所有的服务器和桌面计算机广泛使用。几乎所有的传统个人电脑（PC）和工作站都采用x86架构处理器。x86处理器通常提供更强大的性能，适合高性能计算需求，如桌面电脑、服务器等。相比于ARM处理器，x86处理器的功耗较高，但它们提供了更强的计算能力，因此适用于需要大量计算资源的应用场景。

汇编语言

Assembly is very simple in the sense that it doesn’t have many syntactical constructions compared to high-level programming languages.

相较于高级语言具有很多的语法结构，汇编语言相当简单。主要就是涉及到数据的读取，操作与存储以及指令的跳转。汇编十分接近机器码，我们能够方便的对机器码进行反汇编。

以下是c = a + *b这个功能实现的两种架构汇编实现示例：

;arm
; *a = x0, *b = x1, *c = x2
ldr w0, [x0]    ; load 4 bytes from wherever x0 points into w0
ldr w1, [x1]    ; load 4 bytes from wherever x1 points into w1
add w0, w0, w1  ; add w0 with w1 and save the result to w0
str w0, [x2]    ; write contents of w0 to wherever x2 points

;x86
; *a = rsi, *b = rdi, *c = rdx 
mov eax, DWORD PTR [rsi]  ; load 4 bytes from wherever rsi points into eax
add eax, DWORD PTR [rdi]  ; add whatever is stored at rdi to eax
mov DWORD PTR [rdx], eax  ; write contents of eax to wherever rdx points

我们能发现x86版本加法操作和内存加载在一条指令中同时进行，避免了额外的内存加载指令，这就可以用更少的指令实现更多的功能。而arm代表的RISC架构也有其优点，虽然每个指令只能完成一个操作，但可以通过高效的硬件流水线和指令并行执行来提高总体性能。

后续我们都以x86架构举例：

64、32、16以及8位寄存器的区别一般就体现在名字上（rax,eax,ax,al），其本质上就是使用某个寄存器的低位实现更少位数的寄存器。

寄存器一般分为通用寄存器，浮点寄存器，向量扩展寄存器以及特殊寄存器。向量扩展寄存器通常比普通的通用寄存器要宽，能够存储更多的数据。例如，现代的 x86 CPU 使用 xmm 寄存器来存储 128 位的数据，而 ymm 寄存器则存储 256 位的数据。

立即数就是在指令中出现的一些数字，一般而言会直接嵌入到机器码中，但这无疑增加了机器编码的复杂度，所以有些指令只能使用部分立即数，或者是不能用立即数（只能先加载到寄存器中再进行操作）。

当我们进行数据复制时，比如用mov指令，实际上是一个告诉CPU寄存器更名的过程，由于寄存器重命名的方式，mov 指令不会在 CPU 内部花费额外的时间来复制数据。现代 CPU 在执行指令时，会在内部使用一种称为重命名表（Rename Table）的结构来跟踪寄存器的实际数据位置。当你执行 mov 指令时，CPU 只是更新寄存器映射表，而不进行数据的实际传输。这种操作通常不需要多余的时钟周期，只会消耗一个解码周期（即处理这条指令本身的时间）。xchg指令同理。

地址模式如下：

SIZE PTR [base + index * scale + displacement]

SIZE可以是BYTE,WORD,DWORD以及QWORD，分别对应着1个字节，2个字节，4个字节和8个字节。

scale只能是 1, 2, 4, 或 8。

地址操作一般会用到lea指令，其功能如下：

计算有效地址：lea 指令的主要用途是计算一个内存地址，并将其存储到寄存器中。它不涉及任何实际的内存访问，仅仅是在计算过程中生成内存地址。通常这用于计算复杂的地址，例如数组的偏移。

例如，lea eax, [ebx + 4*ecx] 计算的是 ebx + 4 * ecx 的结果，并将该结果存入 eax 中。这条指令只是计算地址，并没有实际访问 ebx + 4*ecx 所指向的内存位置。

lea除了能获取地址，还能作为算术运算的优化工具

替代乘法和加法：lea 指令还常被作为一个算术优化技巧来替代乘法和加法运算，尤其在需要计算偏移量时非常有用。比如，乘以 3、5 或 9 的运算，可以通过 lea 来实现，避免了直接使用乘法指令（mul）的成本。

例如，如果你需要做 a = b * 3，你通常需要先进行 a = b + b + b 或使用乘法指令。但使用 lea 可以在一条指令中完成相同的计算：lea eax, [ebx + ebx*2]（这里 ebx*2 就是加法的一种优化）。这样就避免了乘法指令，改用了 lea。

作为替代 add 的工具

lea 替代 add：lea 也常常作为 add 指令的替代，尤其是在需要执行多个加法操作时。lea 不需要单独的 mov 指令来保存结果，因为它可以直接将计算结果存入指定寄存器。

例如，假设你有：
1
2
add eax, ebx
add eax, ecx
这两条指令会将 ebx 和 ecx 加到 eax 上。但是，如果你使用 lea，你可以避免使用第二条 add 指令：
1
lea eax, [ebx + ecx]
这条指令会直接将 ebx + ecx 的结果存入 eax，节省了一条 add 指令。通过 lea，你甚至可以在一条指令中执行多个加法运算（如 a = b + c + d），避免了额外的 mov 操作。

上述使用的都是x86汇编的Intel 语法，实际上还存在一种AT&T 语法

AT&T 语法的特点

操作数顺序：在 AT&T 语法中，目标操作数（目的地）在后面，源操作数在前面。例如：movl (%rsi), %eax，意思是将 rsi 寄存器指向的地址中的数据移动到 eax 寄存器。
寄存器和常量的前缀：在 AT&T 语法中，寄存器需要使用 % 前缀（例如 %eax），常量需要使用 $ 前缀（例如 $1）。
内存寻址模式：AT&T 语法中的内存寻址模式是 displacement(%base, %index, scale)，例如 movl 4(%eax, %ebx, 2), %ecx 表示从 eax + ebx * 2 + 4 位置读取数据。
操作数大小后缀：在 AT&T 语法中，操作指令后有大小后缀，表示操作数的大小。常见的后缀有：
- b：字节（8位）
- w：字（16位）
- l：长整型（32位整数或64位浮动点）
- q：四倍长（64位）
- s：单精度浮点数（32位）
- t：十字节（80位浮动点数）

实现*c = *a + *b方式如下：

movl (%rsi), %eax
addl (%rdi), %eax
movl %eax, (%rdx)

循环与条件

循环主要通过跳转指令实现。

跳转指令的作用

跳转指令（如 jmp）的作用是将程序的指令指针（IP）移动到一个新的地址，这个地址由跳转指令的操作数来指定。跳转的目标地址有以下几种可能：

绝对地址：跳转到一个固定的内存地址。
相对地址：跳转到一个相对当前指令位置的地址（例如，跳转前进或后退一定的字节数）。
运行时计算的地址：这个地址不是在编译时固定的，而是在程序运行时计算得到。

标签的使用

为了避免直接管理这些地址，汇编程序员可以使用标签。标签是指用一个字符串标记某个指令的位置，并且这个字符串在机器代码生成时会被替换成相对地址。例如：

start:
    ; 这里是某个指令
    jmp start  ; 跳转回start标签的位置

在上面的例子中，start: 是一个标签，指示 jmp 指令跳转到这个标签的位置。这个标签的实际地址会在编译时被替换为相对地址。

标签的命名规则

标签的命名并不复杂。通常，编译器会使用一些规则来生成标签名称：

行号：编译器可能会使用源代码的行号来生成标签的名称。
函数名：有时，标签会以函数名作为基础，并附加签名信息来标识不同的位置。

这种标签命名方式使得标签的管理变得更清晰，也方便了编译器自动生成跳转目标。

但是单独的往回跳的jmp只会形成类似while(True)的死循环，我们还需搭配条件控制来进行设计循环的边界。

一般是利用FLAGS寄存器来保存比较状态，然后通过该状态来决定是否跳转，常见条件跳转指令有je、jne、ja、jna、jb、jnb等。

循环展开（Loop Unrolling）

由于我们用于循环的指令占一定的长度（循环变量迭代、比较、判断跳转），我们有时候可以通过人为的增加步长并补充必要的有效指令来增加指令的效率，例子如下：

;before optimization
loop:
    add  edx, DWORD PTR [rax]
    add  rax, 4
    cmp  rax, rcx
    jne  loop

;after optimization
loop:
    add  edx, [rax]
    add  edx, [rax+4]
    add  edx, [rax+8]
    add  edx, [rax+12]
    add  rax, 16
    cmp  rax, rcx
    jne  loop

比如我们在遍历一个拥有16个int元素的数组进行求和，我们忽略每个指令实际执行的时间周期花费差异，第一种方法需要16*4=64次指令执行，而第二种方式只用4*7=28次指令执行即可，看上去效率提高了很多。但实际上循环展开不一定带来预期的性能提升，因为现代处理器并不是按顺序一条条执行指令，而是会维护一个指令队列，允许 并行执行独立的操作。这意味着如果两条指令之间没有依赖关系（即它们的执行结果互不影响），处理器可以将它们同时执行，而不需要等待其中一个完成后再执行另一个。

另一种可能的优化思路是利用某些指令的副作用来进行FLAGS位寄存器的设置，从而优化掉cmp的使用。比如利用add结束后会进行的状态设置。

    mov  rax, -100  ; replace 100 with the array size
loop:
    add  edx, DWORD PTR [rax + 100 + rcx]
    add  rax, 4
    jnz  loop       ; checks if the result is zero

常用指令花费

x86 常用指令延迟列表（Latency & Throughput）

指令	延迟（Latency）	吞吐量（Throughput）	说明
`add r/m, r`	1 cycle	1 per cycle	加法
`sub r/m, r`	1 cycle	1 per cycle	减法
`and r/m, r`	1 cycle	1 per cycle	按位与
`or r/m, r`	1 cycle	1 per cycle	按位或
`xor r/m, r`	1 cycle	1 per cycle	按位异或
`cmp r/m, r`	1 cycle	1 per cycle	比较（影响标志位）
`test r/m, r`	1 cycle	1 per cycle	逻辑测试（仅设置标志位）
`mov r, r/m`	1 cycle	1 per cycle	纯寄存器操作的 `mov`
`mov r, imm`	1 cycle	1 per cycle	立即数赋值
`mov r/m, r`	2-3 cycles	0.5 per cycle	可能涉及内存访问
`lea r, [r + r*m + c]`	1-3 cycles	1 per cycle	计算地址，但不访问内存
`imul r, r/m`	3 cycles	1 per 1-3 cycles	有符号整数乘法
`mul r/m`	3-4 cycles	1 per 2-3 cycles	无符号整数乘法
`idiv r/m`	22-30 cycles	1 per 20+ cycles	有符号整数除法（非常慢）
`div r/m`	22-30 cycles	1 per 20+ cycles	无符号整数除法（非常慢）
`sar r/m, imm`	1 cycle	1 per cycle	算术右移
`shl r/m, imm`	1 cycle	1 per cycle	逻辑左移
`shr r/m, imm`	1 cycle	1 per cycle	逻辑右移
`neg r/m`	1 cycle	1 per cycle	取负数
`not r/m`	1 cycle	1 per cycle	取反
`cmovcc r, r/m`	2 cycles	1 per cycle	条件移动（消除分支预测）
`jcc label`（预测正确）	1 cycle	1 per cycle	预测正确的跳转
`jcc label`（预测错误）	~15 cycles	-	预测错误会导致流水线清空
`call label`	4-5 cycles	-	调用函数（压栈）
`ret`	3-4 cycles	-	返回（弹栈）

栈帧结构

rsp存栈顶，rbp存栈底。

栈帧操作所用到的call，ret，push，pop，leave等实际是一种语法糖，其本身可以被拆解为不同的指令组合。

; "push rax"
sub rsp, 8
mov QWORD PTR[rsp], rax

; "pop rax"
mov rax, QWORD PTR[rsp]
add rsp, 8

; "call func"
push rip ; <- instruction pointer (although accessing it like that is probably illegal)
jmp func

; "ret"
pop  rcx ; <- choose any unused register
jmp rcx

; "leave"
mov rsp,rbp
pop rbp

调用约定

传递参数：如 rdi, rsi, rdx, rcx, r8, r9 等寄存器（对于更多的参数，可能会使用栈传递）。

返回值：函数返回值通常存储在 rax 寄存器中。

堆栈管理：在调用其他函数时，通常需要通过 push 和 pop 指令保存和恢复寄存器的内容，以确保函数之间的参数和返回值不会冲突。

每次函数调用时，都可能需要保存寄存器（如 push 和 pop）以及将参数放入寄存器中，尤其是当调用多个函数时，这会增加额外的指令开销。频繁的函数调用，尤其是在性能要求很高的场景中，可能会引入一定的性能损失。

内联优化

内联优化（Inline optimization）是编译器用来提高程序运行效率的一种优化手段。内联优化通过将函数调用替换成函数体的代码，来避免函数调用的开销，从而提高程序的执行效率。

在 C++ 中，内联函数是通过使用 inline 关键字声明的函数。编译器在编译时，会将内联函数的代码直接插入到调用该函数的地方，而不是生成函数调用的代码。这样就避免了常规函数调用的开销（如栈的操作、跳转等）。

inline int square(int x) {
    return x * x;
}

在这个例子中，square 函数会在每次调用时直接将其代码插入到调用点，而不是像普通函数那样产生函数调用的开销。

内联函数的好处

减少函数调用的开销：普通函数调用涉及到参数传递、栈帧的创建、跳转等，内联函数直接替代了函数调用过程，避免了这些开销。
提高执行速度：减少了栈操作和跳转，代码更紧凑，从而提高了执行速度。
减少代码重复：内联函数可以避免重复编写相同的代码块，增强了代码的复用性。

尾调用优化

让我们考虑一个更加复杂的情况，也就是递归调用。

尾递归优化（Tail Call Elimination, TCE）是一种优化技术，它的目的是将尾递归函数转换为迭代（loop），从而避免每次递归调用时额外的栈空间开销。尾递归是指函数调用自己并且在递归调用之后没有其他计算操作，递归的返回值直接就是递归调用的结果。

首先，考虑一个常见的递归阶乘函数：

int factorial(int n) {
    if (n == 0)
        return 1;
    return factorial(n - 1) * n;
}

在这种递归实现中，每次递归调用都需要等待 factorial(n - 1) 计算完成后才进行乘法运算。这个递归调用没有进行尾递归优化，因此每次递归都需要保存返回地址、参数等信息到栈上，直到递归完成才开始计算结果。

对应的汇编实现

; n = edi, ret = eax
factorial:
    test edi, edi       ; 判断 n 是否为零
    jne  nonzero        ; 如果 n 不为零，跳转到 nonzero
    mov  eax, 1         ; 如果 n 为零，返回 1
    ret

nonzero:
    push edi            ; 保存 n，用于后续的乘法
    sub  edi, 1         ; n - 1
    call factorial      ; 递归调用 factorial(n - 1)
    pop  edi            ; 恢复 n
    imul eax, edi       ; 将结果乘以 n
    ret

这个实现是典型的递归形式，每次递归都会保存当前的 n 到栈中，并在递归返回后进行乘法操作。随着递归深度的增加，这会消耗大量的栈空间（push和call分别都会往栈上存1个地址的内容）。

尾递归优化

如果函数是尾递归的（即递归调用之后没有其他操作），我们就可以将递归调用转化为一个循环，这样就避免了递归带来的栈开销。比如我们可以通过引入一个累积参数 p 来进行尾递归优化：

int factorial(int n, int p = 1) {
    if (n == 0)
        return p;
    return factorial(n - 1, p * n);
}

在这个版本中，我们传入一个参数 p 来存储当前的乘积。当 n 为 0 时，直接返回 p。这就避免了递归调用之后的乘法操作，变成了一个可以优化为循环的尾递归。

优化后的汇编实现（尾递归转循环）

; 假设 n > 0
factorial:
    mov  eax, 1         ; 将 eax 初始化为 1（当前乘积）
loop:
    imul eax, edi       ; eax = eax * edi（乘以 n）
    sub  edi, 1         ; n = n - 1
    jne  loop           ; 如果 n != 0，继续循环
    ret

在这个实现中，递归调用被替换成了一个循环。每次循环将当前值 edi（即 n）乘以当前的乘积（存储在 eax 中），然后递减 edi，直到 edi 为 0 时结束。

尾递归优化的好处

节省栈空间：尾递归优化的关键是消除每次递归调用的栈开销。传统递归调用每次都会往栈上压入返回地址、参数等信息，而尾递归优化后，递归实际上被转换成了循环，循环本身不需要额外的栈空间。
提高执行效率：去除了递归调用的开销，避免了函数调用和返回的上下文切换。循环执行通常比递归调用更高效，尤其是在递归深度较大的情况下。

间接分支

在汇编中，所有标签都会转换成绝对或者相对地址然后嵌入指令的机器码中。

多路分支

对于n路分支，一般不会直接创建n个分支，而是创建一个分支函数表来进行定位。switch指令有时候并不能让编译器方便的进行优化，所以像glibc中有关IO部分的实现，一般都会用到goto指令直接跳转。

void weather_in_russia(int season) {
    static const void* table[] = {&&winter, &&spring, &&summer, &&fall};
    goto *table[season];

    winter:
        printf("Freezing\n");
        return;
    spring:
        printf("Dirty\n");
        return;
    summer:
        printf("Dry\n");
        return;
    fall:
        printf("Windy\n");
        return;
}

动态分发（Dynamic Dispatch）

动态分发是实现运行时多态性（runtime polymorphism）的核心技术，尤其在面向对象编程中非常常见。它允许程序在运行时决定调用哪个具体方法，而不是在编译时确定。这种特性使得基于继承和多态的代码结构能够在不同类型的对象上以相同的接口进行操作。

考虑一个经典的例子，我们有一个 Animal 抽象类，其中有一个虚拟的 speak() 方法，以及两个具体实现类：Dog 和 Cat。每个具体类实现了自己的 speak() 方法，Dog 发出 "Bark"，Cat 发出 "Meow"。

struct Animal {
    virtual void speak() { printf("<abstract animal sound>\n"); }
};

struct Dog : public Animal {
    void speak() override { printf("Bark\n"); }
};

struct Cat : public Animal {
    void speak() override { printf("Meow\n"); }
};

创建对象并调用方法

我们希望创建一个 Animal 类型的指针，指向不同的具体对象（Dog 或 Cat），并通过这个指针调用 speak() 方法，而无需在编译时明确知道它指向的是 Dog 还是 Cat。这样，我们可以通过动态分发来调用适当的实现。

int main() {
    srand(time(nullptr));
    Dog sparkles;
    Cat mittens;
    
    Animal* catdog = (rand() & 1) ? static_cast<Animal*>(&sparkles) : static_cast<Animal*>(&mittens);
    catdog->speak();
    return 0;
}

这里我们拿g++编译后的文件扔到IDA里看看，就会发现使用到了vtable来管理函数指针。

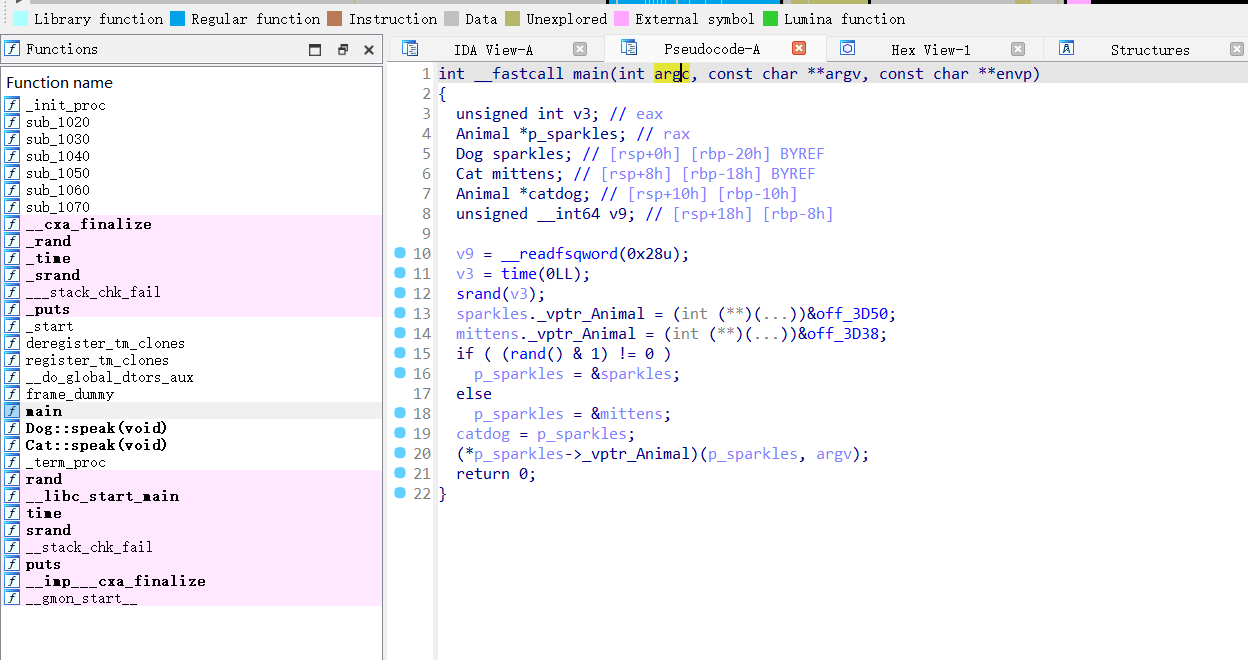
如何实现动态分发

在 C++ 中，动态分发是通过虚拟方法表（vtable）来实现的。下面是它是如何工作的：

虚拟方法表（Vtable）：对于每个实现了虚拟方法的类，编译器会为这个类生成一个虚拟方法表，这个表中包含了该类的所有虚拟方法的地址。表中的每个条目对应类中的一个虚拟方法。
虚拟方法表指针：每个类的实例都会有一个指向其虚拟方法表的指针（通常叫做 vptr）。当你通过 Animal* 指针调用 speak() 方法时，程序会使用该指针的 vptr 来查找正确的虚拟方法表，并从中提取出 speak() 的实际地址。
调用虚拟方法：程序根据对象的 vptr 查找虚拟方法表，从表中找到对应的 speak() 方法地址，然后跳转到该地址执行相应的代码。

虚拟方法表的实现细节

为了保证每个类的虚拟方法调用都能有统一的结构，编译器会使得所有继承自相同基类（比如 Animal）的类具有相同的虚拟方法表结构。具体来说，编译器会将所有虚拟方法的实现调整为相同长度，并可能会在返回指令后插入一些填充指令，确保每个方法的大小一致。

每个类的实例都会包含一个指向其虚拟方法表的指针。通过这个指针，动态分发的调用可以在运行时找到正确的函数。

虚拟方法调用的性能开销

动态分发虽然很强大，但也有一些性能开销：

额外的时间开销：调用虚拟方法时，程序需要通过对象的 vptr 查找虚拟方法表，然后从表中找到正确的函数地址，最后跳转到该函数。这个过程增加了额外的时间开销，通常在大约 15 个周期左右（与分支预测失败类似）。
无法内联：由于虚拟方法调用是在运行时确定的，编译器无法像普通函数那样将其内联，从而失去了内联优化的优势。内联通常可以显著减少函数调用的开销。
类大小增加：每个有虚拟方法的类通常会增加几个字节的空间来存储指向虚拟方法表的指针。这会导致每个对象的大小增加。
二进制文件增大：由于虚拟方法表和其他运行时支持的存在，最终生成的二进制文件通常比不使用多态的代码要大。

机器代码层

CPU的流水线设计一般将其分为前端和后端两个不同的层次结构。前端负责从内存中获取并解码指令。后端负责调度并执行这些指令。在很多情况下，性能瓶颈出现在执行阶段的后端。因为CPU通常可以比执行更快地获取和解码指令，所以优化往往集中在提高执行效率，减少流水线空闲和延迟，并提高指令级并行性。然而，在某些情况下，前端反而会成为瓶颈。这发生在指令获取和解码的速度跟不上后端处理的速度时。即使后端能够处理更多的指令，如果前端没有提供足够的指令，后端就会空闲等待。这种情况通常是由代码布局或指令组织方式引起的。

前端

在前端中，又分为取指阶段（Fetch）和解码阶段（Decode）。

在取指阶段，CPU从主内存中加载固定大小的字节块，这些字节包含了多个指令的二进制编码。这一阶段的目标是将指令从内存取出，准备解码。在x86架构中，这个字节块的大小通常是32字节，但在不同的计算机架构上可能会有所不同。这个块的地址必须是对齐的，也就是说，块的地址必须是其大小的倍数（例如32字节的块地址必须是32的倍数）。CPU通常要求加载的指令块必须按照某种对齐规则存储。对于32字节的块来说，块的起始地址必须是32字节的倍数，否则可能会导致取指过程中的额外延迟。

解码阶段负责将取出的字节块转化为具体的机器指令。CPU会查看这32字节的内容，丢弃当前指令指针之前的部分，然后将剩下的字节切分成指令。机器指令使用可变字节数进行编码。最多可能需要15个字节。一个32字节的块可能解码出多个指令，但解码的数量有一定的机器依赖限制，这个限制被称为解码宽度（decode width）。解码宽度决定了每个周期最多能解码多少条指令。以Zen 2 CPU为例，其解码宽度为4，即每个周期最多可以解码4条指令并将它们传递到下一阶段。

这两个阶段通常是流水线化的工作方式，即前面的阶段不会阻塞后面的阶段。如果CPU能够预测下一块需要加载的指令地址，那么在当前指令块的解码阶段完成之前，取指阶段就会继续加载下一块指令。这种预取机制帮助提高流水线效率，减少CPU等待的时间。

指令缓存（I-cache）

缓存目的：

I-cache 的核心目的是减少 CPU 每次从主内存加载指令的时间。因为直接从主内存获取指令的速度通常比从缓存中读取要慢得多，所以通过引入 I-cache，能够显著减少指令访问延迟。

结构：

I-cache 存储的是指令，而不是数据。它通常由多个 缓存行（cache line） 组成，每个缓存行包含一定数量的指令。缓存的大小和每个缓存行的大小都由硬件架构设计决定。

访问流程：

当 CPU 需要执行某个指令时，它首先检查 I-cache 中是否已有该指令。如果指令已经被缓存（缓存命中），则直接从 I-cache 中取出执行。如果指令不在缓存中（缓存未命中），CPU 就会从主内存中加载该指令，并将其存入 I-cache 中，以便将来使用。这个过程被称为 缓存加载。

缓存一致性：

I-cache 通常是只读的缓存（用于存储指令），不会被 CPU 写操作直接修改。

由于现代处理器有多级缓存（例如 L1、L2、L3 缓存），所以当 I-cache 未命中时，CPU 会逐层向上寻找直到主内存。如果在多级缓存之间找到数据，就会将数据从较高层缓存传递到较低层，直到最终命中的缓存级别。

缓存替换策略：

当 I-cache 中没有足够空间存储新的指令时，CPU 会根据一定的策略替换掉较旧或不常用的指令。常见的替换策略包括： - LRU（Least Recently Used）：替换最久未使用的缓存行。 - FIFO（First In First Out）：按缓存行进入缓存的顺序进行替换。 - Random：随机选择缓存行进行替换。

对性能的影响：

I-cache 的大小和访问策略对 CPU 性能有很大影响。缓存命中率越高，处理器的性能越好。处理器中的 流水线（Pipeline） 和 超标量执行 等技术需要频繁获取指令，因此 I-cache 在高性能处理器中尤其重要。

使用指令缓存后，也会相应影响一些优化策略。

非对称分支

例如有如下C代码，其形式非常对称：

int length(int x, int y) {
    if (x > y)
        return x - y;
    else
        return y - x;
}

但如果我们直接翻译成汇编语言：

length:
    cmp  edi, esi
    jle  less
    ; x > y
    sub  edi, esi
    mov  eax, edi
done:
    ret
less:
    ; x <= y
    sub  esi, edi
    mov  eax, esi
    jmp  done

很明显可以发现，如果x>y，只用5条指令就完成了函数调用；但是如果x<=y，就额外需要经过两次跳转。

其实我们可以假设x>y是不大可能的，然后将如上c代码优化为如下版本：

int length(int x, int y) {
    if (x > y)
        swap(x, y);
    return y - x;
}

其对应汇编如下，显而易见比上述实现方式短了两个指令：

length:
    cmp  edi, esi
    jle  normal     ; if x <= y, no swap is needed, and we can skip the xchg
    xchg edi, esi
normal:
    sub  esi, edi
    mov  eax, esi
    ret

但我们还能进一步优化，我们可以直接认为x>y不可能发生，优化为如下汇编实现：

length:
    cmp  edi, esi
    jg   swap
normal:
    sub  esi, edi
    mov  eax, esi
    ret
swap:
    xchg edi, esi
    jmp normal

这种优化看起来没什么改变，实际上通过把swap提取到正常执行逻辑之外，可以减少跳转的次数，从而节省时间。第一种形式每次都会有 条件跳转（jle），即使在大部分情况下不需要执行交换。而第二种方式在正常情况下不会执行跳转，从而避免了跳转带来的延迟，提升了性能。

对应实现的C代码如下：

int length(int x, int y) {
    if (x > y) [[unlikely]]
        swap(x, y);
    return y - x;
}

三、指令级并行性（ILP）

概述

这里的并行并不是指多核并行，因为多核并行实质上是用多个核心实现计算资源的整合和上限突破，是用计算资源换取效率。这里我们仅考虑一个核心内部的指令并行。执行一条指令大致需要如下5步操作：

取指（IF）
解码（ID）
执行（EX）
存储（MEM）
写回（WB）

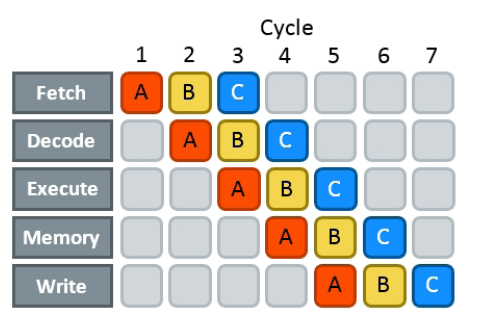
流水线风险

三种主要的流水线风险

结构风险（Structural Hazards）：
- 定义：结构风险发生在两个或多个指令需要相同的CPU资源时。例如，多个指令可能需要访问相同的执行单元（如加法器或乘法器）。如果这个执行单元在某一时刻无法同时处理多条指令，就会发生结构性风险。
- 后果：为了避免冲突，必须等待执行单元空闲后再执行指令，通常这需要额外的一个时钟周期。
- 解决方法：结构风险无法完全避免，它们是性能瓶颈的根源，通常需要通过硬件设计上的调整（例如，增加更多的执行单元）来应对。
数据风险（Data Hazards）：
- 定义：数据风险发生在指令之间存在依赖关系时。例如，某条指令的操作数依赖于前一条指令的计算结果。如果前一条指令还未完成，后续指令就无法执行。
- 后果：这种情况下，必须等待前一条指令计算完成，才能获取必要的数据，这会导致流水线停顿。数据风险的大小取决于关键路径的延迟，即需要等待的数据多久才能计算出来。
- 解决方法：通过重新组织计算顺序来缩短关键路径，避免不必要的等待。例如，重新安排指令的顺序，或者利用数据转发（data forwarding）技术，将计算结果直接传递给后续指令，避免从寄存器读取的延迟。
控制风险（Control Hazards）：
- 定义：控制风险发生在CPU无法预测下一条需要执行的指令时，通常发生在分支指令（如if语句）之后。CPU必须等待条件判断的结果，才能确定接下来的执行路径。
- 后果：如果分支预测失败，CPU通常需要清空流水线，丢弃所有已取指的指令，并重新加载正确的指令，这会浪费15-20个时钟周期。
- 解决方法
  - 消除分支：通过循环展开（loop unrolling）等技术消除分支，从而避免控制风险。
  - 分支预测：通过优化分支预测，使得CPU能够有效猜测分支的方向。现代CPU使用动态分支预测技术，能够根据历史记录预测分支的走向，从而减少控制风险的影响。
  - 分支预测精度：通过改进分支预测算法，使得分支预测更准确，减少流水线清空的次数。

分支预测

分支预测的核心问题正是 CPU 的流水线处理方式导致的。具体来说，现代 CPU 采用指令流水线（pipeline）技术，以提高指令执行的并行度和吞吐量。但在遇到分支指令时，由于目标地址可能依赖于尚未执行完的计算结果，导致 CPU 无法提前确定下一条应该执行的指令，进而产生流水线的停顿。那为什么我们要进行分支预测呢？这是因为如果我们使流水线停顿等待分支条件的计算结果，中间的等待的时间就相对浪费了，那么我们如果知道执行的概率分布，就可以挑一个可能更高的分支进行预执行，那么等到分支条件的计算结果出来之后，如果我们预测成功，相当于高效利用了计算分支条件的这段时间。

case study

假如有如下c代码，假设a数组中等可能随机分布着0-99的数值：

volatile int s;

for (int i = 0; i < N; i++)
    if (a[i] < 50)
        s += a[i];

其在Clang下编译出的结果大致如下：

    mov  rcx, -4000000
    jmp  body
counter:
    add  rcx, 4
    jz   finished   ; "jump if rcx became zero"
body:
    mov  edx, dword ptr [rcx + a + 4000000]
    cmp  edx, 49
    jg   counter
    add  dword ptr [rsp + 12], edx
    jmp  counter

这也是个不对称的分支，如果进入a[i] < 50的这个分支，需要多执行 add dword ptr [rsp + 12], edx 这样一个指令，大约需要多花费4个时钟周期。由于 a[i] 的值是 完全随机的，a[i] < 50 成立的概率大约是 50%。volatile 关键字的作用是防止编译器优化（比如循环展开、向量化等），确保代码执行顺序与写法一致。

现代 CPU 采用 流水线（pipeline）技术，在执行一条指令时，会提前加载下一条指令。但如果遇到不可预测的分支，就会出现 分支预测失败（Branch Misprediction），导致 CPU 清空流水线，重新加载正确的指令。

在 AMD Zen 2 上：

CPU 的流水线大约有 19 个阶段，如果分支预测失败，就需要 19 个周期 来填充流水线。
每次循环：
1. 读取数组值（memory load）+ 比较（compare）：大约需要 5 个周期。
2. 加法操作（如果满足条件）：大约需要 4 个周期。
3. 50% 预测失败的情况下，每 2 次循环需要清空流水线一次（19 个周期）。

那么，每两个元素的平均执行时间是：这与实验测得的 14 个周期/循环 完全一致，说明 分支预测失败 是主要的性能瓶颈。如果我们改变分支的比较条件为小于P，则能得到图表如下：

最大值在50处，这比较直观，因为50%概率相当于完全随机选取一个分支进行预取执行，很容易分支预测失败并丢弃整个流水线重新加载。最小值在P=0处，此时相当于每次必不进入分支，那每次基本就只用检查一下条件是否满足。而有一个极小值在85-90%左右，这是因为进入分支会多执行加法操作，会多花约4 个周期。超过了这个转折点，多执行的加法操作代价就超过了10%概率丢弃流水线的代价了。

模式识别

前面我们讨论了 分支预测失败（Branch Misprediction） 对性能的影响。在 P=50%（也就是 a[i] 以 50% 的概率小于 50）的情况下，由于数据是随机分布的，CPU 无法准确预测 if (a[i] < 50) 语句的走向，因此 每次预测失败都会导致流水线清空，最终导致 14 cycles/element 的低效执行。

1. 排序优化

我们可以在计算前 先对数组进行排序：

for (int i = 0; i < N; i++)
    a[i] = rand() % 100;

std::sort(a, a + N);

这样，数组 a 变成了一个 递增序列：

[0, 1, 2, ..., 49, 50, ..., 99]

这意味着：

前半部分 (a[i] < 50) 连续执行 "yes" 分支。
后半部分 (a[i] >= 50) 连续执行 "no" 分支。

这时，CPU 的分支预测器可以轻松适应这个模式：

在前 50% 的数据里，分支总是跳转到 s += a[i] 语句。
在后 50% 的数据里，分支总是不进入加法逻辑。

因为 CPU 的 动态分支预测器（Dynamic Branch Predictor） 能检测到“连续命中”模式，所以流水线 几乎不会被清空，这样每个元素的计算只需要 4 cycles，而不是 14 cycles。

2. 预测器如何学习更复杂的模式？

现代 CPU 的分支预测器远比 “历史统计” 更先进。它们不仅会记录某个分支的过去走向，还会识别更复杂的执行模式。

实验 1：减少 N 的大小 如果我们把数组大小 N 减少到 1000，但不排序：

for (int i = 0; i < 1000; i++)
    a[i] = rand() % 100;

此时，CPU 可以完全记住所有 1000 个数据点的分支模式：

因为 分支预测器的历史表（BTB, Branch Target Buffer）能够存储足够多的历史信息，它可以记住 每个 a[i] < 50 的位置，从而 100% 预测成功。
这样，CPU 根本不会犯错，分支预测 几乎完美，导致 执行时间降到 4 cycles/element 以下！

分支提示

如果我们事先知道某个分支更可能被执行，可以 显式地告诉编译器，让它优化指令布局，使 CPU 处理分支更快。

C++20 引入了 [[likely]] 关键字，可以用于指示某个分支更有可能被执行：

for (int i = 0; i < N; i++)
    if (a[i] < P) [[likely]]  // 提示这个分支更可能执行
        s += a[i];

当 P=75 时：

使用 [[likely]]：执行速度 ≈ 7.3 cycles/element
不使用 [[likely]]：执行速度 ≈ 8.3 cycles/element

提升了约 1 cycle 的效率。

[[likely]] 并不会直接影响 CPU 的分支预测器，而是改变了汇编代码的布局，使 CPU 前端（Front-End）更容易处理常见分支。也就是使更可能执行的分支紧跟主代码路径（减少 jmp 跳转的开销）。

在 C++20 之前，也可以使用 __builtin_expect（GCC & Clang 支持）：

#define LIKELY(x) __builtin_expect(!!(x), 1)
#define UNLIKELY(x) __builtin_expect(!!(x), 0)

for (int i = 0; i < N; i++)
    if (LIKELY(a[i] < P))
        s += a[i];

少分支编程

既然进行分支预测可能会导致整个流水线清空重载，那么我们很容易想尝试能不能不用或少用分支实现同样的功能。

比如还是上述例子：

for (int i = 0; i < N; i++)
    a[i] = rand() % 100;

volatile int s;

for (int i = 0; i < N; i++)
    if (a[i] < 50)
        s += a[i];

可以用如下方法进行优化，去除掉if语句。

for (int i = 0; i < N; i++)
    s += (a[i] < 50) * a[i];

汇编中没有布尔类型，也没有直接建立正负值到0，1的映射。但是我们可以通过位操作技巧来实现这个功能，也就是右移位31位（因为int类型占32位）。这样由于负数的补码表示中最高位为1，所以可以用来建立一个正负值到0，1的映射。

; x = a[i]
mov  ebx, eax   ; t = x
sub  ebx, 50    ; t -= 50
sar  ebx, 31    ; t >>= 31
imul  eax, ebx   ; x *= t
add dword ptr [rsp + 12], eax	; s+=x

由于imul需要花费3个cycle，于是有种花费2个cycle实现的方式：

mov  ebx, eax   ; t = x
sub  ebx, 50    ; t -= 50
sar  ebx, 31    ; t >>= 31
; imul  eax, ebx ; x *= t
sub  ebx, 1     ; t -= 1 (causing underflow if t = 0)
and  eax, ebx   ; x &= t
add dword ptr [rsp + 12], eax	; s+=x

但上述两种优化方式没有考虑下溢出的情况，也就是这个范围内的值减50后会溢出，从而导致进入错误的分支。

所以现代 CPU 提供了一种条件移动（Conditional Move, cmov）指令，能避免乘法和位运算，提高效率：

mov     ebx, 0      ; cmov 不能直接使用立即数，所以先设定 ebx=0
cmp     eax, 50
cmovge  eax, ebx    ; 若 eax >= 50，则 eax = ebx (0)

这相当于：

s += (a[i] < 50 ? a[i] : 0);

最终编译器优化的汇编代码：

mov     eax, 0
mov     ecx, -4000000
loop:
    mov     esi, dword ptr [rdx + a + 4000000]  ; 读取 a[i]
    cmp     esi, 50
    cmovge  esi, eax                            ; esi = (esi >= 50 ? 0 : esi)
    add     dword ptr [rsp + 12], esi           ; s += esi
    add     rdx, 4
    jnz     loop                                ; 继续循环

决定何时用分支

由于cmov的方式实际上还是会让流水线产生暂停，这里我们可以对比一下两种不同方式在不同P值情况下的效率。可以看出当有75%把握确定选取某个分支时，分支预测的效率实际是会优于无分支方式的。

应用示例

字符串处理

在简化的情况下，std::string 实际上是由指向一个以 null 结尾的字符数组（也就是 C 字符串）的指针，以及一个存储字符串大小的整数组成的。一个常见的字符串值是空字符串，它的默认值也是空字符串。

处理空字符串的传统方式是，将字符串的指针赋为 nullptr，并将字符串大小赋为 0。在处理字符串时，我们需要检查指针是否为空或者大小是否为零。这样就会引入一个分支（if 检查），这种分支会带来性能开销（尤其是在大多数字符串为空或非空的情况下）。

为了去除这个分支，我们可以为空字符串分配一个“零 C 字符串”，即分配一个包含零字节的内存，并将所有空字符串都指向这个零字节。这样，所有处理空字符串的操作都将读取这个无用的零字节，虽然这会增加一些操作，但仍然比一个分支预测错误的开销要小得多。

二分查找

标准的二分查找可以通过消除分支来实现，在处理小数组（适合缓存时）时，比使用分支的 std::lower_bound 快大约 4 倍。

以下是一个消除分支的二分查找实现：

int lower_bound(int x) {
    int *base = t, len = n;
    while (len > 1) {
        int half = len / 2;
        base += (base[half - 1] < x) * half;  // 会被替换成 "cmov"
        len -= half;
    }
    return *base;
}

这个实现的复杂度略高，但它的一个缺点是它可能会进行更多的比较（比标准二分查找需要更多的比较），并且无法像传统二分查找那样进行未来内存读取的预测（这通常作为预取操作，因此在处理非常大的数组时会有所损失）。

总结来说，数据结构通过隐式或显式地填充数据，消除分支，使得其操作需要固定次数的迭代。更多复杂的示例可以参考相关资料。

数据并行编程

在 SIMD（单指令多数据）应用中，分支消除非常重要，因为 SIMD 本身不支持分支操作。

在我们之前的数组求和例子中，去除累加器的 volatile 类型修饰符后，编译器能够对循环进行向量化优化：

/* volatile */ int s = 0;

for (int i = 0; i < N; i++)
    if (a[i] < 50)
        s += a[i];

向量化后的代码每个元素处理时间为 0.3 个周期，性能瓶颈主要来自内存访问。

编译器通常能够向量化任何没有分支或迭代之间没有依赖关系的循环。如果循环存在少量的复杂变体，例如包含只有一个 if 而没有 else 的简单循环，编译器也能进行向量化优化。但对于更复杂的循环，向量化则变得非常复杂，可能需要一些技术，例如掩码处理和寄存器内的重新排列。

指令表

在数字电子学中，交错执行（Interleaving execution stages）是一种常见的优化方式，它不仅应用于 CPU 的主流水线（pipeline），还用于单个指令的执行单元以及内存操作。大多数执行单元都有自己的小型流水线，并且通常可以在前一条指令执行一两周期后，就接受另一条指令。

在现代 CPU 体系结构中，执行单元（Execution Units）是处理特定类型指令的硬件模块。不同的指令类别通常由专门的执行单元处理。例如：

整数运算单元（ALU, Arithmetic Logic Unit）：用于执行 add、sub、cmp 等整数运算。
浮点运算单元（FPU, Floating Point Unit）：用于执行 mulss、divss 等浮点数运算。
加载/存储单元（Load/Store Unit, LSU）：用于 mov r, m、mov m, r 等内存访问指令。
分支单元（Branch Unit）：用于 jmp、call、ret 等控制流指令。

这些执行单元通常也是流水线化的（Pipelined），并且现代 CPU 可能会有多个相同类型的执行单元，以提高吞吐量。可以把 CPU 的流水线看作是多个层级的流水线结构。

以下是一些常见的 CPU 资源分配：

流水线阶段	可能涉及的硬件单元
取指（IF）	指令缓存（L1I Cache）、IFU取指单元
解码（ID）	指令解码单元、寄存器重命名单元
执行（EX）	ALU（整数运算）、FPU（浮点运算）、SIMD（矢量指令）、AGU（地址计算单元）
访存（MEM）	LSU（加载/存储单元）、L1/L2 Cache
写回（WB）	寄存器文件、提交队列

所以在这种情况下，有两种不同衡量指令花费的标准，一种是延迟（Latency），另一种是吞吐量（Throughput）。

延迟（Latency）：指令的执行结果需要多少个周期（cycles）才能获得。
吞吐量（Throughput）：平均每个周期可以执行多少条该指令。

对于特定的 CPU 架构，我们可以通过指令表（Instruction Tables）来获取这些数值。以下是 AMD Zen 2 架构上一些指令的示例（所有操作数均为 32 位）：

指令	延迟（Latency）	反向吞吐量（Reciprocal Throughput）
`jmp`	-	2
`mov r, r`	-	1/4
`mov r, m`	4	1/2
`mov m, r`	3	1
`add`	1	1/3
`cmp`	1	1/4
`popcnt`	1	1/4
`mul`	3	1
`div`	13-28	13-28

吞吐量的倒数（Reciprocal Throughput）

因为人们通常习惯于“数值越大代表开销越大”的成本模型，所以更常用反向吞吐量（Reciprocal Throughput），即每条指令平均需要多少个周期才能执行完一条（而不是每周期执行多少条）。

指令执行单元的复用

如果某条指令非常频繁，CPU 可能会复制其执行单元，以提高吞吐量（但通常不会超过解码宽度）。
例如，add 具有 1/3 的吞吐量，这表示多个 add 指令可以在不同的执行单元中同时进行。

流水线执行

许多指令都是流水线化（Pipelined）的。例如，如果某条指令的吞吐量倒数是 n，通常意味着它的执行单元可以在 n 个周期后接受另一条同样的指令。
如果吞吐量倒数小于 1（如 mov r, r 的 1/4），表示 CPU 可能有多个执行单元，可以在同一周期并行执行多条这样的指令。

变量延迟（Variable Latency）

某些指令的延迟会根据操作数的值和大小而变化。
内存访问指令（如 mov r, m）的延迟通常按最优情况（L1 缓存命中）计算。如果数据来自 L2 或者更慢的内存层级，延迟会显著增加。

优化延迟通常和优化吞吐量有很大的不同，

假设有一个数组求和的代码：

int s = 0;
for (int i = 0; i < n; i++)
    s += a[i];

如果我们假设：

编译器没有向量化（SIMD 没有被使用）。
访存不是瓶颈（假设数据已在 L1 缓存中）。
循环已展开（即手动展开循环，消除循环变量维护的额外开销）。

那么，它会被展开成：

int s = 0;
s += a[0];
s += a[1];
s += a[2];
s += a[3];
// ...

由于 add 指令的延迟为 1，每次 s += a[i] 操作都依赖于前一次计算的 s，导致只能每个周期执行 1 次 add，即 处理 1 个数组元素/周期。

然而，我们注意到 Zen 2 处理器的 add 吞吐量是 2，也就是说 CPU 实际上每个周期可以执行 2 次 add，但当前代码无法利用这个能力，因为每个 add 依赖于上一次的 s，存在数据依赖。这里说add的吞吐量为2，好像与上面表中说明吞吐量为3相悖，实际是因为寄存器到寄存器的 add 指令吞吐量很高（4），但如果 add 的操作数之一来自内存，它的执行速度就会受到内存读取的吞吐量限制（2）。

假设 CPU 里有 4 条 ALU 管道 专门用于 add 操作，而有 2 条 Load/Store 单元（LSU） 用于 mov（内存加载）。

如果 add 只用 ALU（reg, reg），它可以 4 条并行执行。
如果 add 需要访问内存（reg, [mem]），它必须先经过 LSU 加载数据，但 LSU 只有 2 条管道，所以吞吐量上限是 2。

你可以把 add reg, reg 想象成 一条 4 车道的高速公路，而 add reg, [mem] 受限于 2 车道的收费站，所以即使后面有 4 车道，整体吞吐量还是受限于 2 车道的瓶颈。

解决方案：使用多个累加器

为了提高吞吐量，我们可以使用两个独立的累加器，分别求和奇数索引和偶数索引的元素：

int s0 = 0, s1 = 0;
s0 += a[0];
s1 += a[1];
s0 += a[2];
s1 += a[3];
// ...
int s = s0 + s1;

这样做的好处是：

s0 和 s1 互不依赖，可以并行执行。
由于 add 吞吐量是 2，CPU 每个周期可以执行 2 条 add 指令，所以数组求和的吞吐量提高了一倍。
计算完成后，我们再执行 s0 + s1，这只是一次额外的 add，不会显著影响性能。

一般情况：多累加器策略

如果某条指令：

延迟（Latency）= x
吞吐量（Throughput）= y

那么，要完全利用 CPU 的执行单元，我们需要 x × y 个独立的累加器，以确保 CPU 在任何时刻都有足够的指令可以执行，不会被数据依赖阻塞。

对于 add：

Latency = 1
Throughput = 2

因此，我们需要1 × 2 = 2 个累加器（s0 和 s1），刚好匹配 CPU 资源，最大化吞吐量。

在优化循环时，我们通常：

确定 CPU 关键的执行端口（Execution Ports）—— 不同指令可能使用不同的执行端口。
分析循环中各个指令的吞吐量，找出最可能成为瓶颈的指令。
使用机器代码分析工具（如 LLVM's llvm-mca、Intel VTune、uops.info）来查看哪条指令最占用资源，然后针对性优化。

Collectcrop's Blog

Algorithmica-HPC研读记录1

Algorithmica HPC研读记录（1-3章）

一、复杂性模型

概述

传统复杂性理论

渐进分析理论

现代硬件

编程语言

二、计算机架构

指令集架构（ISA）

汇编语言

循环与条件

循环展开（Loop Unrolling）

常用指令花费

栈帧结构

调用约定

内联优化

尾调用优化

间接分支

多路分支

动态分发（Dynamic Dispatch）

机器代码层

前端

指令缓存（I-cache）

非对称分支

三、指令级并行性（ILP）

概述

流水线风险

分支预测

case study

模式识别

分支提示

少分支编程

决定何时用分支

应用示例

字符串处理

二分查找

数据并行编程

指令表